MT【273】2014新课标压轴题之$\ln2$的估计

已知函数$f(x)=e^x-e^{-x}-2x$
(1)讨论$f(x)$的单调性;
(2)设$g(x)=f(2x)-4bf(x),$当$x>0$时,$g(x)>0,$求$b$的最大值;
(3)已知$1.4142<\sqrt{2}<1.4143$,估计$\ln 2$的近似值(精确到0.001）.

分析:(1)$f^{'}(x)=e^x+e^{-x}-2\ge2\sqrt{e^x\cdot e^{-x}}-2=0$,故$f(x)$在$R$上单调递增.
(2)$g(x)=e^{2x}-e^{-2x}-4x-4b(e^x-e^{-x}-2x),$
$g^{'}(x)=2e^{2x}+2e^{-2x}-4-4b(e^x+e^{-x}-2)=2(e^x+e^{-x}-2)(e^x+e^{-x}+2-2b)$,
设$h(x)=e^x+e^{-x}+2-2b,h(0)=4-2b$
当$b\le 2$时,易知$h(x)\ge h(0)=0,$故$g(x)$在$(0,+\infty)$上单调递增,由$g(0)=0$知,$g(x)>0$,满足题意.
当$b>2$时,存在零点$\phi$,使得$h(\phi)=0,\phi=\ln(b-1+\sqrt{b^2-2b})$,故$g(x)$在$(0,\phi)$单调递减,又$g(0)=0,$故$g(x)<0$,不符合题意.
综上,$b$的最大值为2.
(3)首先应该要知道$\ln 2$的大概值为0.693(平时的积累,类似要知道$\pi\approx3.1415926$.)这里选择的函数应该是带有$b$的$g(x)$ 而不是$f(x)$, 其次要估计$\ln 2$ 又要用到$\sqrt{2}$, 由$g(x)$ 的函数形式,$x$ 的取值很容易尝试$ln\sqrt{2},g(\ln\sqrt{2})=(4b-2)\ln2+\dfrac{3}{2}-2\sqrt{2}b$, 当$b\in(\dfrac{1}{2},2]$ 时 由$g(\ln\sqrt{2})>0$ 得$\ln 2>\dfrac{2\sqrt{2}b-\dfrac{3}{2}}{4b-2}\ge\dfrac{8\sqrt{2}-3}{12}>0.6928$
上界尝试在当$b>2$时估计.令$\phi=\ln2$,此时$b=\dfrac{3\sqrt{2}}{4}+1$,由(2)知$g(\ln\sqrt{2})<g(0)=0,$ 得
$\ln 2<\dfrac{2\sqrt{2}b-\dfrac{3}{2}}{4b-2}=\dfrac{18+\sqrt{2}}{28}<0.6934.$
故$\ln2\approx 0.693$

练习:

附解答:

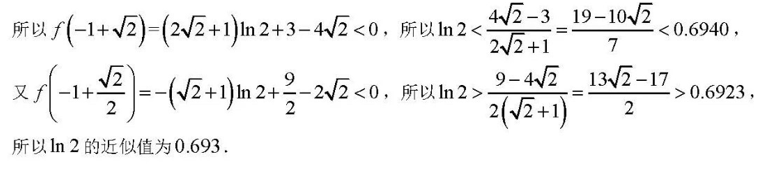
注:泰勒展开$\ln(1+x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\cdots+(-1)^{n-1}\dfrac{x^n}{n}+o(x^n)$

故$ln(\dfrac{1+x}{1-x})=2(x+\dfrac{x^3}{3}+\cdots)$取$x=\dfrac{1}{3}$则$ln(2)\approx 0.693$