bzoj3756pty的字符串(后缀自动机+计数)

题目描述

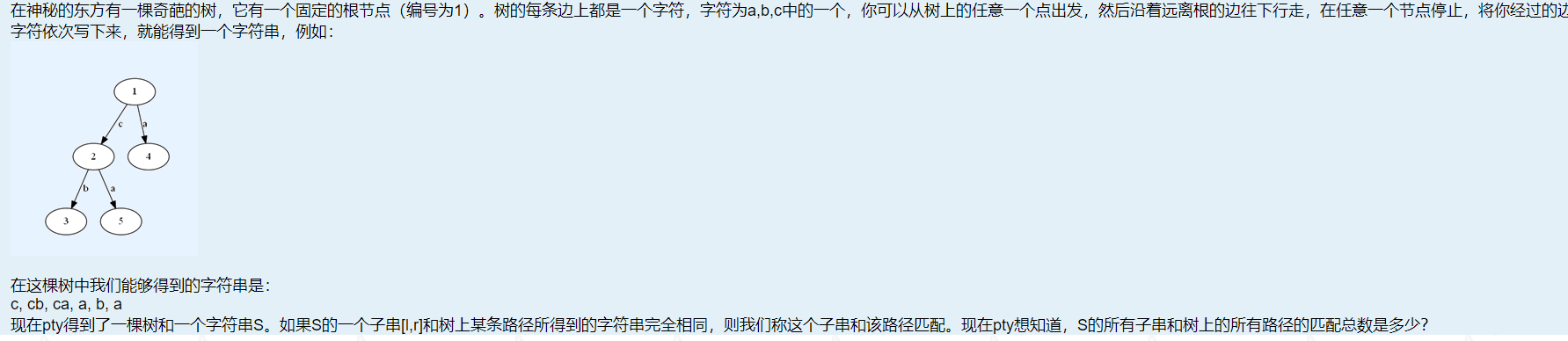
题解

我们可以先对trie树建出广义SAM，然后维护一下right集合大小(注意right集合在广义SAM上的维护方式)。

然后把匹配穿往广义SAM上匹配，假设现在匹配到了x节点，那么x的所有祖先后可以被匹配上，那么一个节点的贡献即为r[x]*(l[x]-l[fa[x]])。

维护这玩意的和就好了，最下面的节点特判一下。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 1600002
#define M 8000002
using namespace std;
typedef long long ll;
char c[],s[M];
int cnt,n,father,pa[N],len,tong[N],rnk[N];
ll sum[N],ans;
int l[N],ch[N][],fa[N],r[N];
inline int rd(){
    int x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(c=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
inline int ins(int last,int x){
    int p=last;
    if(ch[p][x]){
        int q=ch[p][x];
        if(l[p]+==l[q]){r[q]++;return q;}
        else{
            int nq=++cnt;l[nq]=l[p]+;r[nq]=;//care!!!!!!!!!!!!!!!
            memcpy(ch[nq],ch[q],sizeof(ch[q]));
            fa[nq]=fa[q];fa[q]=nq;
            for(;ch[p][x]==q;p=fa[p])ch[p][x]=nq;
            return nq;
        }
    }
    else{
        int np=++cnt;l[np]=l[p]+;r[np]=;
        for(;p&&!ch[p][x];p=fa[p])ch[p][x]=np;
        if(!p)fa[np]=;
        else{
            int q=ch[p][x];
            if(l[p]+==l[q])fa[np]=q;
            else{
                int nq=++cnt;l[nq]=l[p]+;
                memcpy(ch[nq],ch[q],sizeof(ch[q]));
                fa[nq]=fa[q];fa[q]=fa[np]=nq;
                for(;ch[p][x]==q;p=fa[p])ch[p][x]=nq;
            }
        }
        return np;
    }
}
int main(){
    n=rd();cnt=;pa[]=;
    for(int i=;i<=n;++i){
        father=rd();scanf("%s",c);
        pa[i]=ins(pa[father],c[]-'a');
    }
    scanf("%s",s+);len=strlen(s+);
    for(int i=;i<=cnt;++i)tong[l[i]]++;
    for(int i=;i<=n;++i)tong[i]+=tong[i-];
    for(int i=;i<=cnt;++i)rnk[tong[l[i]]--]=i;
    for(int i=cnt;i>=;--i){int x=rnk[i];r[fa[x]]+=r[x];}
    r[]=;
    for(int i=;i<=cnt;++i){int x=rnk[i];sum[x]=sum[fa[x]]+1ll*(l[x]-l[fa[x]])*r[x];}
    int now=,le=;
    for(int i=;i<=len;++i){
        if(ch[now][s[i]-'a'])le++,now=ch[now][s[i]-'a'];
        else{
            for(;now&&!ch[now][s[i]-'a'];now=fa[now]);
            if(now)le=l[now]+,now=ch[now][s[i]-'a'];
            else le=,now=;
        }
        if(now!=)ans+=sum[fa[now]]+1ll*(le-l[fa[now]])*r[now];
    }
    cout<<ans;
    return ;
}

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 1600002
#define M 8000002
using namespace std;
typedef long long ll;
char c[],s[M];
int cnt,n,father,pa[N],len,tong[N],rnk[N];
ll sum[N],ans;
int l[N],ch[N][],fa[N],r[N];
inline int rd(){
    int x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(c=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
inline int ins(int last,int x){
    int p=last;
    if(ch[p][x]){
        int q=ch[p][x];
        if(l[p]+==l[q]){r[q]++;return q;}
        else{
            int nq=++cnt;l[nq]=l[p]+;r[nq]=;//care!!!!!!!!!!!!!!!
            memcpy(ch[nq],ch[q],sizeof(ch[q]));
            fa[nq]=fa[q];fa[q]=nq;
            for(;ch[p][x]==q;p=fa[p])ch[p][x]=nq;
            return nq;
        }
    }
    else{
        int np=++cnt;l[np]=l[p]+;r[np]=;
        for(;p&&!ch[p][x];p=fa[p])ch[p][x]=np;
        if(!p)fa[np]=;
        else{
            int q=ch[p][x];
            if(l[p]+==l[q])fa[np]=q;
            else{
                int nq=++cnt;l[nq]=l[p]+;
                memcpy(ch[nq],ch[q],sizeof(ch[q]));
                fa[nq]=fa[q];fa[q]=fa[np]=nq;
                for(;ch[p][x]==q;p=fa[p])ch[p][x]=nq;
            }
        }
        return np;
    }
}
int main(){
    n=rd();cnt=;pa[]=;
    for(int i=;i<=n;++i){
        father=rd();scanf("%s",c);
        pa[i]=ins(pa[father],c[]-'a');
    }
    scanf("%s",s+);len=strlen(s+);
    for(int i=;i<=cnt;++i)tong[l[i]]++;
    for(int i=;i<=n;++i)tong[i]+=tong[i-];
    for(int i=;i<=cnt;++i)rnk[tong[l[i]]--]=i;
    for(int i=cnt;i>=;--i){int x=rnk[i];r[fa[x]]+=r[x];}
    r[]=;
    for(int i=;i<=cnt;++i){int x=rnk[i];sum[x]=sum[fa[x]]+1ll*(l[x]-l[fa[x]])*r[x];}
    int now=,le=;
    for(int i=;i<=len;++i){
        if(ch[now][s[i]-'a'])le++,now=ch[now][s[i]-'a'];
        else{
            for(;now&&!ch[now][s[i]-'a'];now=fa[now]);
            if(now)le=l[now]+,now=ch[now][s[i]-'a'];
            else le=,now=;
        }
        if(now!=)ans+=sum[fa[now]]+1ll*(le-l[fa[now]])*r[now];
    }
    cout<<ans;
    return ;
}