利用python 学习数据分析 (学习三)
内容学习自:
Python for Data Analysis, 2nd Edition
就是这本
纯英文学的很累,对不对取决于百度翻译了
前情提要:
各种方法贴:
https://www.cnblogs.com/baili-luoyun/p/10250177.html
本节内容,numpy 结尾, 以及pands初入门
一:伪随机函数
samples =np.random.normal(size=(3,3))
print(samples)
samples1 =np.random.seed(1234) #调节随机种子
print(samples1) >>>> [[ 0.91041087 0.99724402 -0.0681944 ]
[ 0.48277059 -1.50446272 0.30656754]
[-0.01929894 -0.27835256 -0.68331925]]
None
2>:给上下限的数取整
samplse1 = np.random.randint(1,6) #给上下限的数取整数
print(samplse1)
.>>>.>>>>>
# 随机整数
2
3>:产生正太分布样本
arr1 =np.random.randn(3,3) #产生正态分布的样本值
print(arr1) >>>>>
[[ 0.55526507 -0.3952732 1.49921319]
[-0.06943318 -0.05375604 -0.26636376]
[-1.48909115 -0.00702559 0.15973251]]
4>:产生均匀分布样本
arr1 =np.random.rand(3,3) #产生均匀分布的样本质
print(arr1)
>>>
[[0.56847387 0.23533505 0.97136229]
[0.0049996 0.60753788 0.20997453]
[0.41777576 0.26264969 0.55777828]]


二:随机漫步
1:单随机漫步(普通方法)
import matplotlib.pylab as plt
import random
postition = 0
walk =[postition]
steps =1000
for i in range(steps):
step = 1 if random.randint(0,1) else -1
postition += step
walk.append(postition)
print(walk)
plt.plot(walk[:100])
plt.show() >>>>>>
[0, 1, 0, 1, 2, 1, 0, -1, 0, -1, -2, -3, -4, -5, -6, -5, -6, -5, -6, -7, -8, -7, -8, -7, -8, -7, -6, -5, -6, -7, -6, -7, -8, -7, -8, -9, -8, -7, -6, -5, -6, -5, -4, -3, -4, -3, -2, -3, -4, -5, -4, -5, -4, -5, -6, -5, -4, -3, -4, -5, -4, -3, -2, -3, -2, -1, -2, -1, -2, -3, -4, -5, -4, -3, -2, -3, -4, -3, -2, -1, 0, 1, 0, -1, 0, -1, 0, 1, 2, 3, 4, 5, 4, 3, 2, 3, 2, 1, 2, 1, 0, 1, 2, 3, 4, 3, 4, 3, 4, 3, 4, 3, 4, 5, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1, 2, 3, 4, 3, 4, 5, 6, 5, 4, 5, 4, 5, 6, 5, 6, 5, 4, 3, 2, 1, 2, 1, 0, 1, 0, -1, 0, 1, 0, -1, -2, -1, -2, -1, 0, 1, 2, 3, 4, 5, 4, 5, 4, 3, 4, 5, 6, 7, 8, 7, 6, 5, 4, 5, 6, 7, 6, 7, 6, 7, 8, 9, 10, 9, 8, 9, 8, 9, 10, 11, 10, 11, 12, 11, 10, 9, 10, 9, 8, 7, 8, 7, 6, 5, 4, 5, 4, 3, 2, 1, 0, 1, 0, 1, 2, 1, 0, -1, 0, -1, -2, -3, -2, -1, 0, 1, 0, 1, 0, -1, 0, 1, 0, -1, -2, -3, -2, -3, -2, -3, -4, -3, -2, -3, -4, -3, -2, -3, -4, -3, -4, -3, -2, -3, -4, -3, -4, -5, -6, -7, -6, -7, -8, -9, -10, -9, -8, -7, -8, -9, -10, -11, -12, -13, -14, -15, -14, -15, -14, -15, -14, -13, -12, -13, -14, -13, -14, -15, -16, -17, -18, -17, -18, -19, -18, -19, -20, -19, -18, -17, -16, -15, -14, -13, -12, -11, -12, -13, -12, -13, -12, -11, -10, -9, -8, -9, -8, -7, -8, -9, -10, -9, -10, -11, -12, -13, -12, -13, -14, -13, -12, -13, -14, -15, -14, -13, -12, -11, -12, -13, -12, -13, -12, -13, -14, -13, -14, -15, -14, -15, -16, -17, -16, -15, -16, -15, -16, -15, -16, -17, -18, -17, -18, -19, -18, -17, -16, -15, -14, -15, -14, -15, -16, -17, -18, -19, -20, -21, -20, -21, -20, -19, -20, -19, -18, -19, -18, -17, -16, -17, -16, -15, -16, -15, -14, -15, -14, -15, -14, -15, -16, -15, -14, -15, -16, -17, -16, -15, -16, -15, -16, -17, -16, -15, -14, -13, -14, -15, -14, -13, -14, -15, -16, -17, -16, -15, -14, -13, -12, -13, -14, -15, -14, -15, -14, -13, -12, -11, -12, -11, -12, -13, -14, -13, -12, -13, -12, -13, -14, -13, -14, -15, -14, -15, -14, -13, -12, -13, -14, -15, -14, -15, -16, -15, -16, -17, -18, -17, -18, -17, -18, -17, -18, -17, -18, -19, -18, -19, -18, -17, -18, -19, -20, -19, -18, -19, -18, -17, -16, -15, -14, -15, -16, -15, -14, -15, -16, -15, -16, -15, -14, -13, -12, -11, -12, -11, -10, -11, -12, -13, -14, -13, -12, -11, -10, -11, -10, -11, -12, -13, -14, -15, -14, -15, -14, -15, -16, -17, -16, -17, -18, -17, -18, -17, -16, -15, -14, -15, -14, -15, -16, -15, -14, -15, -16, -17, -18, -19, -20, -21, -20, -19, -18, -19, -18, -17, -18, -19, -18, -19, -18, -19, -20, -19, -18, -19, -20, -19, -20, -19, -18, -19, -20, -21, -22, -21, -22, -23, -22, -21, -20, -21, -20, -21, -22, -21, -20, -19, -18, -19, -18, -19, -18, -17, -18, -19, -20, -21, -20, -21, -22, -23, -24, -23, -22, -21, -20, -19, -20, -19, -18, -17, -18, -17, -18, -19, -20, -21, -20, -19, -18, -19, -20, -21, -22, -23, -22, -23, -22, -21, -20, -21, -22, -23, -24, -25, -24, -25, -24, -25, -24, -25, -26, -25, -24, -25, -26, -25, -26, -27, -28, -29, -30, -29, -30, -31, -32, -33, -34, -33, -32, -33, -34, -33, -34, -33, -32, -31, -30, -29, -30, -31, -30, -31, -30, -29, -28, -27, -26, -27, -28, -27, -26, -25, -24, -25, -26, -25, -24, -25, -24, -23, -22, -23, -22, -21, -20, -21, -20, -21, -20, -19, -20, -19, -20, -21, -22, -21, -20, -19, -20, -19, -18, -19, -18, -17, -16, -15, -16, -17, -18, -19, -20, -21, -22, -23, -22, -23, -24, -25, -26, -27, -28, -29, -28, -27, -28, -27, -26, -25, -24, -25, -26, -27, -26, -27, -26, -25, -24, -23, -24, -25, -24, -25, -26, -25, -26, -27, -28, -27, -26, -27, -26, -25, -24, -25, -26, -25, -26, -27, -28, -27, -28, -27, -26, -27, -26, -27, -26, -25, -24, -25, -24, -23, -22, -21, -20, -21, -20, -21, -22, -21, -20, -21, -20, -19, -20, -21, -20, -19, -20, -21, -22, -23, -24, -23, -22, -21, -22, -23, -24, -25, -26, -25, -24, -23, -24, -23, -22, -23, -22, -23, -22, -21, -20, -21, -22, -23, -24, -23, -22, -21, -22, -21, -22, -21, -20, -19, -20, -19, -20, -21, -22, -21, -20, -19, -18, -19, -18, -17, -18, -19, -20, -19, -20, -21, -20, -19, -20, -19, -18, -19, -20, -19, -20, -19, -18, -19, -18, -17, -18, -17, -18, -19, -18, -17, -16, -15, -16, -15, -16, -15, -14, -15, -16, -17, -18, -19, -20, -19, -18, -17, -16, -17, -18, -19, -20, -21, -20, -19, -20, -21, -20, -21, -20, -21, -22, -21, -20, -19, -20, -21, -20, -19, -20, -21, -22, -21, -22, -23, -24, -23, -24, -23, -24, -23, -24, -25, -26, -27, -28, -27, -28, -29, -30, -29, -28, -27, -26, -27, -26, -27, -28, -29, -28, -27, -26, -27, -28, -29, -30, -29, -30, -31, -32, -31, -32, -31, -30, -29, -30, -31, -30, -29, -28, -29, -30, -29, -28, -27, -28, -27, -26, -25, -26, -25, -26, -25, -24, -25, -26, -27, -26, -27, -26, -25, -24, -25, -26, -25, -24, -25, -24, -23, -22, -23, -24]
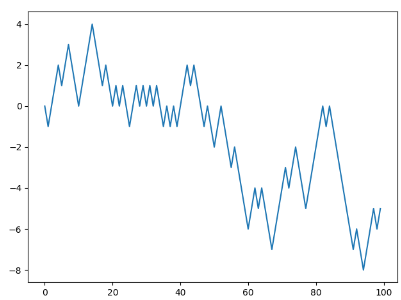
2:利用numpy随机漫步
1>:生产1个0 或者1 的1维矩阵,1000次
nsteps =1000
draws =np.random.randint(0,2,size=nsteps) #生成一个0 或者1 的1位矩阵,1000次
print(draws)
>>>>
[1 1 1 0 1 1 1 0 1 0 0 0 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 0 0 0 0 0 1 1 1 0 0.............. 0 1 1 1 0 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 1 0 0 1 1 0 1
1]
2>:进行三元运算累加
nsteps =1000
draws =np.random.randint(0,2,size=nsteps) #生成一个0 或者1 的1位矩阵,1000次
# print(draws)
steps =np.where(draws>0 ,1,-1) #三元运算
walk =steps.cumsum() #累加
print(walk)
plt.plot(walk)
plt.show()
>>>>>>>>>>
[ 1 0 -1 0 -1 0 -1 0 1 0 1 2 3 4 3 4 5 6
5 6 5 4 5 6 7 6 7 8 9 10 11 10 11 12 11 10
11 12 11 12 11 12 13 14 13 12 13 14 15 16 15 16 17 18
17 18 17 18 19 18 17 16 15 14 15 16 17 16 15 14 13 12
11 10 9 10 9 10 9 10 9 10 9 10 11 10 11 12 11 10
9 10 11 12 11 10 9 10 11 10 9 8 9 8 9 8 9 8
.......

2.1>最大值 ,最小值
l1 =walk.min() # 最小值
print(l1)
l2 =walk.max() #最大值
print(l2)
>>>>>>
-51
12
2.2>求距离0 到(+,-)10 距离最近的索引
l =(np.abs(walk)>=10).argmax() #求距离0 位置10个距离的索引
print(l)
\>>>>>>>>>>>>>>
35
3:模拟多次随机漫步
nwalks =5000 #组数
nsteps =1000 #步数
draws =np.random.randint(0,2,size=(nwalks,nsteps)) # 生成1,0 内的随机5000个漫步值
print(draws)
steps =np.where(draws>0 ,1,-1)
walks =steps.cumsum(1)
print(walks)
>>>>
[[1 1 1 ... 1 0 1]
[0 0 0 ... 0 1 1]
[1 0 0 ... 0 1 0]
...
[0 0 0 ... 1 0 0]
[1 1 0 ... 0 1 1]
[1 0 1 ... 0 0 1]]
[[ 1 2 3 ... 54 53 54]
[ -1 -2 -3 ... -50 -49 -48]
[ 1 0 -1 ... -34 -33 -34]
...
[ -1 -2 -3 ... -64 -65 -66]
[ 1 2 1 ... -8 -7 -6]
[ 1 0 1 ... -8 -9 -8]]
利用python 学习数据分析 (学习三)的更多相关文章
- "利用python进行数据分析"学习记录01
"利用python进行数据分析"学习记录 --day01 08/02 与书相关的资料在 http://github.com/wesm/pydata-book pandas 的2名字 ...
- Python: 利用Python进行数据分析 学习记录
-----15:18 2016/10/14----- 1. import numpy as np;import pandas as pd values = pd.Series(np.random.no ...
- PYTHON学习(三)之利用python进行数据分析(1)---准备工作
学习一门语言就是不断实践,python是目前用于数据分析最流行的语言,我最近买了本书<利用python进行数据分析>(Wes McKinney著),还去图书馆借了本<Python数据 ...
- 利用python进行数据分析——(一)库的学习
总结一下自己对python常用包:Numpy,Pandas,Matplotlib,Scipy,Scikit-learn 一. Numpy: 标准安装的Python中用列表(list)保存一组值,可以用 ...
- $《利用Python进行数据分析》学习笔记系列——IPython
本文主要介绍IPython这样一个交互工具的基本用法. 1. 简介 IPython是<利用Python进行数据分析>一书中主要用到的Python开发环境,简单来说是对原生python交互环 ...
- 利用python进行数据分析--(阅读笔记一)
以此记录阅读和学习<利用Python进行数据分析>这本书中的觉得重要的点! 第一章:准备工作 1.一组新闻文章可以被处理为一张词频表,这张词频表可以用于情感分析. 2.大多数软件是由两部分 ...
- 参考《利用Python进行数据分析(第二版)》高清中文PDF+高清英文PDF+源代码
第2版针对Python 3.6进行全面修订和更新,涵盖新版的pandas.NumPy.IPython和Jupyter,并增加大量实际案例,可以帮助高效解决一系列数据分析问题. 第2版中的主要更新了Py ...
- 利用Python进行数据分析_Pandas_基本功能
申明:本系列文章是自己在学习<利用Python进行数据分析>这本书的过程中,为了方便后期自己巩固知识而整理. 第一 重新索引 Series的reindex方法 In [15]: obj = ...
- 利用Python进行数据分析(第二版)电子版书籍分享
资料下载地址: 链接:https://pan.baidu.com/s/1y1C0bJPkSn7Sv6Eq9G5_Ug 提取码:vscu <利用Python进行数据分析(第二版)>高清中文版 ...
- 利用Python进行数据分析 2017 第二版 项目代码
最近在学习<利用Python进行数据分析>,找到了github项目的地址, 英文版本,中文版本 (非常感谢翻译中文的作者). mark一下,方便后边学习查找.
随机推荐
- 10-SSH综合案例:前台用户模块:邮箱服务器配置
之前发邮件是自己发到服务器还是?是自己搭建一个还是注册一个163啊?自己可以搭建一个邮箱的服务器然后去发送邮件.就是你必须得在这上面有了账户才能发,你也可以往网络上发.你的主机就是一台邮箱服务器了.你 ...
- Python_02-控制语句
目录: 1 控制结构... 1.1 分支语句... 1.1.1 if语句的嵌套... 1.2 for循环... 1.2.1 Python 循环中的 ...
- windows 安装git
搭建环境:windo server 2012 方案: 服务器端:gitblit.下载地址:http://www.gitblit.com/ 客户端:git for windows.下载地址:https: ...
- http://classworlds.codehaus.org/apiusage.html
API Usage The Java API can be used to create new realms and connect realms together through importat ...
- static变量和static函数
在C语言编程中,static的一个作用是信息屏蔽! 比方说,你自己定义了一个文件 -- 该文件中有一系列的函数以及变量的声明和定义! 你希望该文件中的一些函数和变量只能被该文件中的函数使用,那么,你可 ...
- XSS学习笔记
本片文章是读<<XSS跨站脚本gj剖析与防御>>一书的总结 常见的XSS攻击主要用于1.网络钓鱼,盗用用户账号2.窃取cookies 非httponly情况下,读取docume ...
- Ansible常用模块命令
Ansible常用模块命令 一.安装ansible yum install epel-release yum install ansible 二.配置文件配置 vi /etc/ansible/ansi ...
- mongo学习- mapReduce操作事例
源数据: { "_id" : 1.0, "name" : "abc", "age" : 43.0, "type ...
- [在职软件工程]基于CMMI的软件工程教程
第1章 软件工程基础 1.1软件工程基本原理 a.按照软件生命周期的阶段划分制定计划,严格依据计划进行管理 项目概要计划,里程碑计划,项目控制计划,产品控制计划,验证计划,运行维护计划 b.坚持进行阶 ...
- linux相关文章链接
薄荷开元网 http://www.mintos.org/
