CART回归树

决策树算法原理(ID3，C4.5)

决策树算法原理(CART分类树)

决策树的剪枝

　　CART回归树模型表达式：

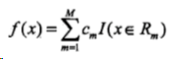
　　其中，数据空间被划分为R₁~R_m单元，每个单元有一个固定的输出值C_m。这样可以计算模型输出值与真实值的误差：

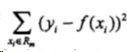
　　希望每个单元上的C_m，可以使平方误差最小化，易知当C_m为相应单元上所有实际值的均值时，达到最优：

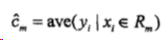
　　如何生成这些被划分的单元？

　　下面是一组数据：

　　选择变量x_j为切分变量，它的取值s为切分点，那么得到两个区域：

　　当 j 和 s 固定时，我们要找到两个区域的代表值C₁、C₂使各自区间上的平方差最小，

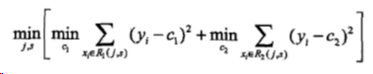
　　已经知道C₁、C₂为区间上的平均，

　　那么对固定的 j 只需要找到最优的 s，
　　然后通过遍历所有的变量，我们可以找到最优的 j，
　　这样我们就可以得到最优对（j，s），并得到两个区间。

　　上述过程表示的算法步骤：

　　即：

1. 考虑数据集 D 上的所有特征 j，遍历每一个特征下所有可能的取值或者切分点 s，将数据集 D 划分成两部分 D1 和 D2。
2. 分别计算上述两个子集的平方误差和，选择最小的平方误差对应的特征与分割点，生成两个子节点。
3. 对上述两个子节点递归调用步骤1、2,直到满足停止条件。
    

来自：https://www.jianshu.com/p/b90a9ce05b28