清北学堂模拟赛d1t4 一道图论好题(graph)

题目描述

LYK有一张无向图G={V,E}，这张无向图有n个点m条边组成。并且这是一张带权图，不仅有边权还有点权。

LYK给出了一个子图的定义，一张图G’={V’,E’}被称作G的子图，当且仅当

·G’的点集V’包含于G的点集V。

·对于E中的任意两个点a,b∈V’，当(a,b)∈E时，(a,b)一定也属于E’，并且连接这两个点的边的边权是一样的。

LYK给一个子图定义了它的价值，它的价值为：点权之和与边权之和的比。

LYK想找到一个价值最大的非空子图，所以它来找你帮忙啦。

输入格式(graph.in)

第一行两个数n,m表示一张n个点m条边的图。

第二行n个数ai表示点权。

接下来m行每行三个数u,v,z，表示有一条连接u,v的边权为z的无向边。数据保证任意两个点之间最多一条边相连，并且不存在自环。

输出格式(graph.out)

你需要输出这个价值最大的非空子图的价值，由于它是一个浮点数，你只需要保留小数点后两位有效数字。

输入样例

3 3

2 3 4

1 2 3

1 3 4

2 3 5

输出样例

1.67

样例解释

选择1,2两个点，则价值为5/3=1.67。

对于20%的数据n=2

对于50%的数据n<=5

对于100%的数据1<=n,m<=100000，1<=ai,z<=1000。

分析：对于前50%的数据我们只需要枚举每个点选或不选就可以了.在搜索的时候打个表，就能看出一点规律：最后一定只选两个点！

为什么呢？观察这样一个图: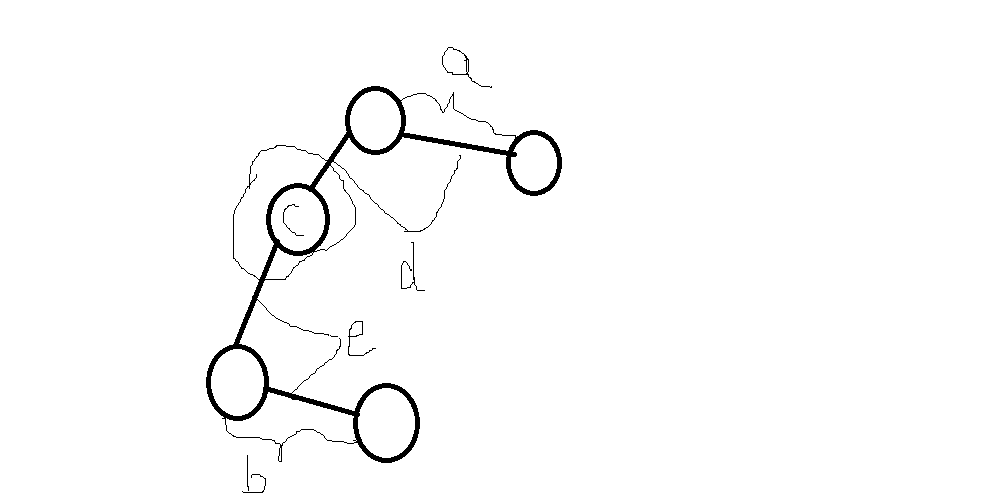

如果选所有点，那么答案为(a+b+c)/(d + e),如果选上面一部分的点，那么答案为(a + c) / d,选取下面一部分点答案为(c + b) / e,可以证明，选取上面或者选取下面总有一个答案比选取整个要大，所以我们每次选更小的子图，直到只剩下两个点，这两个点肯定是点权和/边权最大的两个点.

如果数据跳的特别大，那么很有可能就是有规律，先从小数据暴力打表，最后推移到大数据上，再转化为小数据来做.

#include <bits/stdc++.h>

using namespace std;

int n,m,a[];

struct node
{
    int u,v,w;
    double p;
}e[];

bool cmp(node a,node b)
{
    return a.p < b.p;
}

int main()
{
    freopen("graph.in","r",stdin);
    freopen("graph.out","w",stdout);
    scanf("%d%d",&n,&m);
    for (int i = ; i <= n; i++)
        scanf("%d",&a[i]);
    for (int i = ; i <= m; i++)
    {
        scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
        e[i].p = (double)(a[e[i].u] + a[e[i].v]) / e[i].w;
    }
    sort(e + ,e +  + m,cmp);
    printf("%.2lf",e[m].p);

    return ;
}