短时程突触可塑性(short-term synaptic plasticity)
介绍
神经元的突触可塑性一般被认为是大脑学习与记忆的分子生物学机制,它是指突触传递效率增强或减弱的变化现象。若这种变化只持续数十毫秒到几分,便称之为短时程突触可塑性,其中效率增强与减弱分别叫做短时程增强(short-term enhancement)与短时程抑制(short-term depressed);而持续数百毫秒的增强又被称之为短时程易化( short-term facilitation)
易化与抑制是2种并存的机制,他们的共同作用对神经系统的信息传递起到至关重要的作用。因此,研究短时程突触可塑性具有重要意义。
短期突触可塑性或短期可塑性与长期可塑性不同。 首先,短期可塑性运行的时间尺度远小于长期可塑性的时间尺度,可能与网络动力学的时间尺度相当。 其次,给定突触的短期可塑性是由传入尖峰序列(突触前相关性)中的相关性驱动的,而经典长期塑性是由突触前和突触后活性的相关性驱动的; 后者的一个突出的例子是赫伯的学习规则(Hebb,1949; Gerstner&van Hemmen,1993)。
对短期可塑性进行建模是基于这样的想法:需要某种“资源”来跨越突触间隙传递动作电位(Liley&North,1953; Magleby&Zengel 1975; Abbott等人,1997; Tsodyks&Markram ,1997; Varela等,1997)。 术语“资源”可以解释为神经递质的可用量,某种离子浓度梯度或突触后受体密度或可用性。 我们假设动作电位的每一次传输都会影响可用突触资源的数量,可用资源的数量决定了传输的有效性,从而决定了突触后电位的最大值。
建模短时程抑制
建模短时程抑制。 基于一阶反应动力学的简单模型已经反复证明可以用来定量描述神经肌肉接头处的短期可塑性(Liley&North,1953; Magleby&Zengel,1975)和皮层突触(Tsodyks&Markram 1997; Varela 1997)。 Tsodyks和Markram(1997)的模型假设了三种可能的状态:突触连接的“资源”:有效,无效和恢复。 只要动作电位到达突触,恢复的资源的固定部分R首先变为有效,然后不活动,并最终恢复。 在这些状态之间的转换通过使用时间常数tinact和trec的一级动力学来描述。 实际的突触后电流与有效资源量成比例。
在脉冲响应模型的背景下,三态模型可以被简化,因为突触后电流的时间过程,正如从有效到无效状态的转变所描述的那样,已经被形式的由响应函数给出的突触后电位。唯一相关的数量是由单个动作电位提供的电荷确定的PSP的最大(最小)。由有效和无效到恢复状态的转换由线性微分方程描述,PSP的最大值仅取决于进入的动作电位实际激活的资源量。因此,我们可以总结有效的两步恢复资源,最终形成一个有效(Z)和无效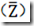 资源的双态模型。每个进入的动作可能性将瞬时切换活动资源的比例R到非活动状态,从那里恢复到时间常数为t的活动状态;见图1A。从形式上看,
资源的双态模型。每个进入的动作可能性将瞬时切换活动资源的比例R到非活动状态,从那里恢复到时间常数为t的活动状态;见图1A。从形式上看,
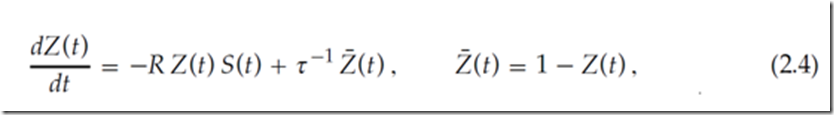
其中S(t)= Σfδ(t-tf) 是输入脉冲序列。 该微分等式被很好地定义,如果我们申明Z(t)是左连续的,即Z(tf):=Z(tf-0)
在单次传输中释放的费用以及PSP的最大费用取决于切换到非活动状态的资源的数量,或者等同于紧接在传输之前的活动资源的数量。 那么t时刻突触的强度就是Z(t)的函数,我们简单地把J(t)= J0Z(t)放在其中J0是所有资源处于活动状态的最大突触强度。
现在让我们假设第一个脉冲在t0时刻到达突触。 紧接在尖峰到达之前,所有资源都处于活动状态,并且Z(t0)= 1。动作电位将资源的一小部分R切换到非活动状态,使得Z(t0+0)= 1-R.动作电位的到来,不活跃的资源在t快速恢复,我们有
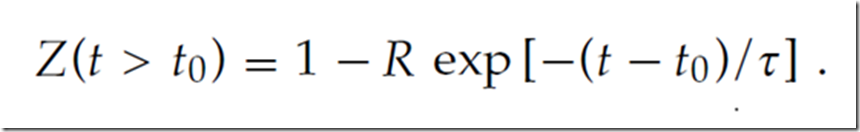
在随后的脉冲的到达时刻t1,只有Z(t1)资源处于活动状态,并且PSP相应地抑制(见图2A和2B)。
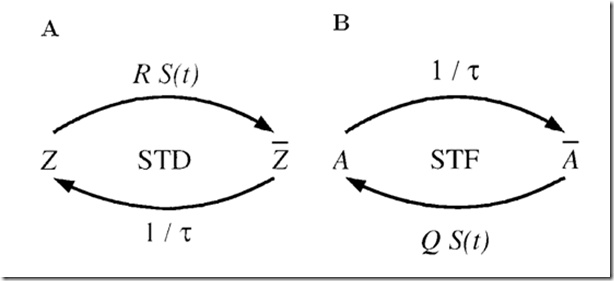
目前的短期抑制模型(A)和短期促进(B)的示意图。 随着短期抑制,每一个进入的动作电位将活动资源Z的比例R切换到非活动状态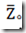 这被表示为具有时间依赖率R S(t)的一阶反应动力学; 这里S是即将到来的脉冲序列。 从非激活状态,资源随时间常数t放松到活动状态。 短期促进的模型通过反转箭头的方向而从短期抑郁的模型中出现。 表示无效的资源,通过传入的脉冲以QS(t)的速率抽取。 活动资源A以速率τ(-1)放松回到非活动状态。
这被表示为具有时间依赖率R S(t)的一阶反应动力学; 这里S是即将到来的脉冲序列。 从非激活状态,资源随时间常数t放松到活动状态。 短期促进的模型通过反转箭头的方向而从短期抑郁的模型中出现。 表示无效的资源,通过传入的脉冲以QS(t)的速率抽取。 活动资源A以速率τ(-1)放松回到非活动状态。
从前面的几个例子中,我们可以很容易地读出一个复发关系,它将紧接在第n个峰值之前的活动资源量与前一个峰值的量关联起来,
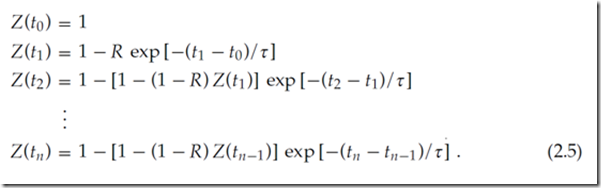
顺便说一句,我们注意到替代Z(t0)=1,我们可以采用任何想要的初始条件0<t0≤1. 随后的论点并没有改变.
循环关系(见等式2.5)是Z(tn)=an+bnZ(tn-1) 的形式,其中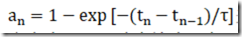 并且
并且 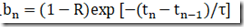 递归替换和简短计算会产生以下显式表达式,表示活动资源的数量,
递归替换和简短计算会产生以下显式表达式,表示活动资源的数量,
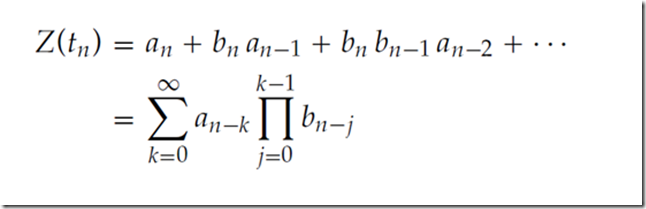
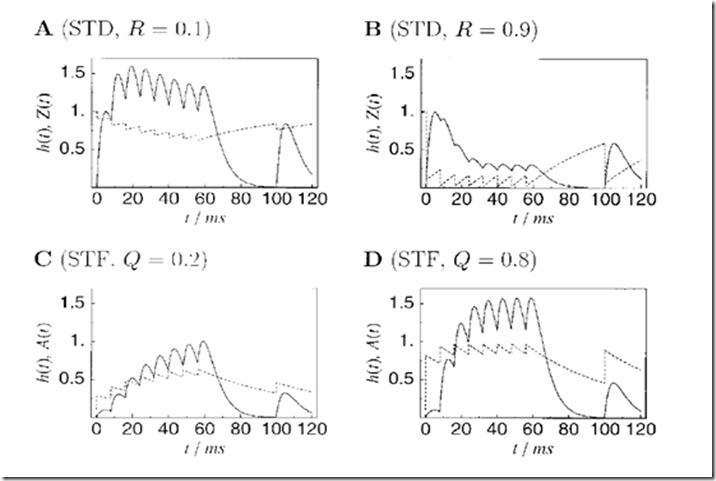
在短期抑制(A,B)和促进(C,D)的情况下,膜电位(实线)和突触强度(虚线)作为时间的函数。 在(A)中,在单个传输期间仅使用所有可用资源的一小部分R=0.1,使得突触仅受发送器耗尽的影响。 在(B)中,参数R增加到R=0.9。 这导致了突触强度的显着的短期抑制。 A0=0.1,Q=0.2(C)和A0=0.1,Q=0.8(D)的下面两个图表说明了短期促进。 对于所有的数字,突触恢复的时间常数是t=50毫秒,EPSP的上升时间等于5毫秒。 峰值到达0,8,16,。。。 ,56ms,最后在t=100ms。
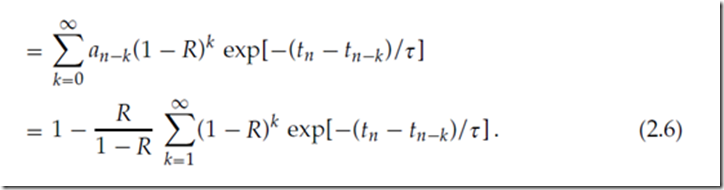

短期促进化建模
以类似的方式,我们可以设计一个模型来解释短期的促进而不是抑制。 为此,我们假设在没有突触前尖峰的情况下,活动突触资源A(t)的分数随时间常数τ衰减。 每个来料加标从无效资源库 中招募一定比例Q; 见图1B。 那么A(t)的动态是
中招募一定比例Q; 见图1B。 那么A(t)的动态是
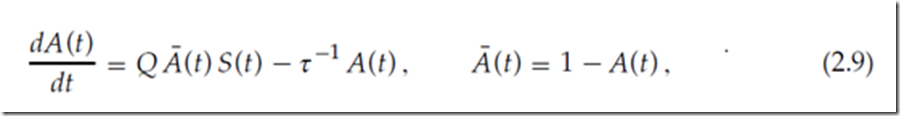
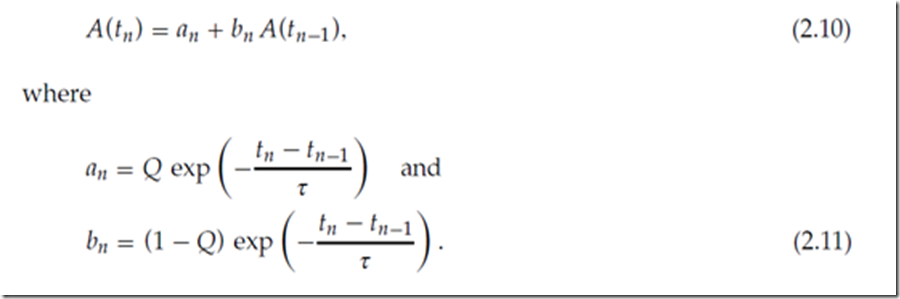

短时程突触可塑性(short-term synaptic plasticity)的更多相关文章
- LSTM学习—Long Short Term Memory networks
原文链接:https://colah.github.io/posts/2015-08-Understanding-LSTMs/ Understanding LSTM Networks Recurren ...
- LSTM(Long Short Term Memory)
长时依赖是这样的一个问题,当预测点与依赖的相关信息距离比较远的时候,就难以学到该相关信息.例如在句子”我出生在法国,……,我会说法语“中,若要预测末尾”法语“,我们需要用到上下文”法国“.理论上,递归 ...
- 时间序列(六): 炙手可热的RNN: LSTM
目录 炙手可热的LSTM 引言 RNN的问题 恐怖的指数函数 梯度消失* 解决方案 LSTM 设计初衷 LSTM原理 门限控制* LSTM 的 BPTT 参考文献: 炙手可热的LSTM 引言 上一讲说 ...
- 用PHP实现URL转换短网址的算法示例
短网址就是把一个长的地址转换在超级短的网址,然后访问短网址即可跳转到长网址了,下面来看用PHP实现URL转换短网址的算法与例子. 短网址(Short URL) ,顾名思义就是在形式上比较短的网址.在W ...
- Linux应急响应(二):捕捉短连接
0x00 前言 短连接(short connnection)是相对于长连接而言的概念,指的是在数据传送过程中,只在需要发送数据时,才去建立一个连接,数据发送完成后,则断开此连接,即每次连接只完成一 ...
- 长网址 短网址(http://www.zhihu.com/question/19852154?rf=21975802)
短网址(Short URL),顾名思义就是在形式上比较短的网址.通常用的是asp或者php转向,在Web 2.0的今天,不得不说,这是一个潮流.目前已经有许多类似服务,借助短网址您可以用简短的网址替代 ...
- 短URL链接系统
定义: 短网址(Short URL),顾名思义就是在形式上比较短的网址.但不知道有多少人像我一样,由于面试问道才知道有这种系统而对短连接原理好奇,从而进行进一步的研究.在Web 2.0的今天,不得不说 ...
- 二维码及二维码接合短URL的应用
二维码 1.什么是二维码? 二维条形码,最早发明于日本,它是用某种特定的几何图形按一定规律在平面(二维方向上)分布的黑白相间的图形记录数据符号信息的,在代码编制上巧妙地利用构成计算机内部逻辑基础的“0 ...
- URL短网址生成算法原理和php实现案例
短网址(Short URL),顾名思义就是在形式上比较短的网址. 短链接的好处:1.内容需要:2.用户友好:3.便于管理为什么要这样做的,原因我想有这样几点:微博限制字数为140字一条,那么如果我们需 ...
随机推荐
- 熊猫猪新系统測试之四:Ubuntu 14.04
眼下猫猪在办公室一般用的就是乌班图系统,一方面原因是老本本性能跑不起来Windows,更重要的是本猫认为Linux系统更开放些.况且如今用的也比較熟了,全然能够脱离Windows鸟!这一系列4篇新系统 ...
- php权威编程有趣部分
1.isset empty如果遇到null,isset判断为false;empty 判断为trueisset(var1, var2,...) 可以判断多个变量 2.unsetunset可以取消之前定义 ...
- python-mysql-replication
python处理mysql binlog增量日志 http://python-mysql-replication.readthedocs.io/en/latest/examples.html 同样的项 ...
- Android Asynchronous Http Client 中文教程
本文为译文,原文链接https://loopj.com/android-async-http/ 安卓异步httpclient 概述 这是一个异步的基于回调的Android http客户端,构建于Apa ...
- 1、硬件IO口配置;
对于MTK TP驱动移植一般分为六部分: 1.硬件IO口配置: 2.TP驱动移植. 3.I2C通信: 4.中断触发: 5.数据上报: 6.虚拟按键. 硬件电路: 1.GPIO配置 打开 mediate ...
- Xcode强大的多视图立体分层显示View UI Herarchy
Xcode能够显示执行页面的立体uivew结构图,能够让你看到一个页面包括哪些视图,在哪一层,在页面的什么位置. 一看就能看到你的uiview是否显示.显示在哪里了. 用鼠标点击页面移动鼠标能够看到页 ...
- openstack-计算节点安装(Node)
感谢朋友支持本博客,欢迎共同探讨交流.因为能力和时间有限.错误之处在所难免,欢迎指正. 假设转载,请保留作者信息. 博客地址:http://blog.csdn.net/qq_21398167 原博文地 ...
- Install RabbitMQ server in CentOS 7
About RabbitMQ RabbitMQ is an open source message broker software, also sometimes known as message-o ...
- java 实现统计某段文字在内容中出现的次数
http://outofmemory.cn/code-snippet/815/java-zishutongji 一个api,位于apache.commons.lang.StringUtils类下的一个 ...
- Unicode utf8等编码类型的原理
1.ASCII码 我们知道,在计算机内部,所有的信息最终都表示为一个二进制的字符串.每一个二进制位(bit)有0和1两种状态,因此八个二进制位就可以组合出256种状态,这被称为一个字节(byte). ...
