Hidden Markov Models笔记

Andrew Ng CS229 讲义： https://pan.baidu.com/s/12zMYBY1NLzkluHNeMNO6MQ

HMM模型常用于NLP、语音等领域。

• 马尔科夫模型（Markov Model）

只有状态序列z。状态转移矩阵A。

有限视野假设（limited horizon assumption），Markov性：

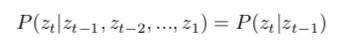
静态过程假设（stationary process assumption），参数时不变性：

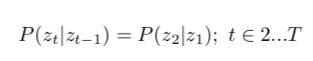
两个问题：1）概率问题，2）学习问题

问题1）概率问题：已知转移矩阵A，求某观测状态序列z的概率是多少

根据有限视野假设，

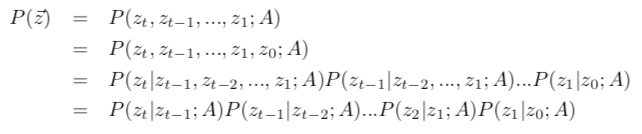
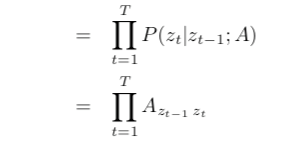
带入计算即可。

问题2）学习问题：已知观测状态序列z，求参数A最大化z出现的概率

使用最大似然估计，最大化log似然函数

即求解问题

转化为Lagrange multipliers：

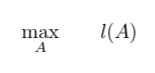
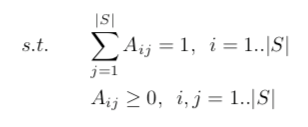
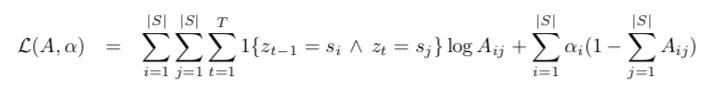
分别对参数求偏导并令其为零：

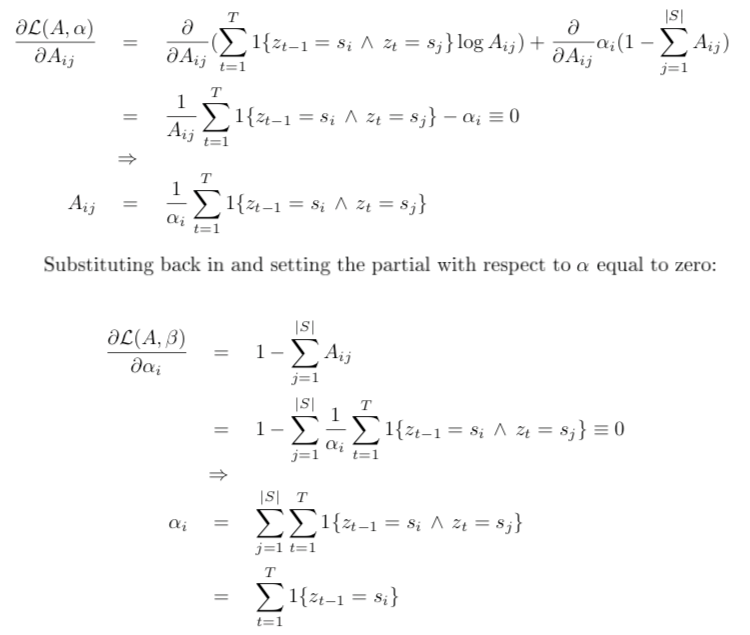
代入得到状态转移矩阵A的估计：

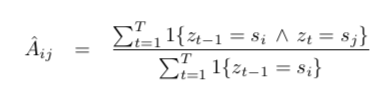
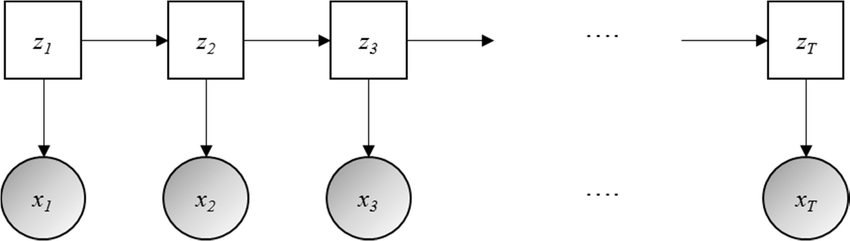
• 隐马尔科夫模型（Hidden Markov Model）

状态序列z，观测序列x。状态转移矩阵A，发射（生成输出）矩阵B。

输出独立假设（output independence assumption）：

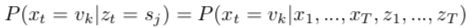
三个问题：1）概率问题，2）解码问题，3）学习问题

1）概率问题：已知转移矩阵A、发射矩阵B，求观测序列x的概率 - 前向算法

根据输出独立假设，

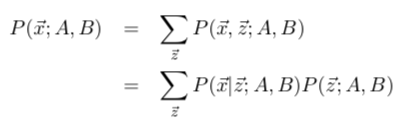
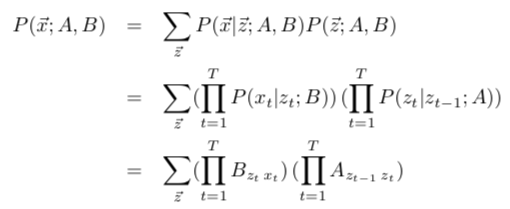
更快的做法是动态规划，即前向算法。

定义

重新推导概率：

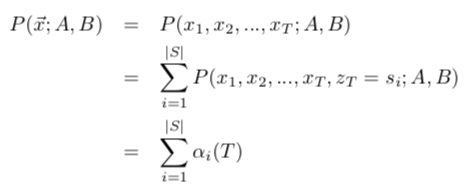
类似地，对应有后向算法：

2）解码问题：已知转移矩阵A、发射矩阵B，观测序列x，求状态序列z的概率 - Viterbi算法

使用贝叶斯定理：

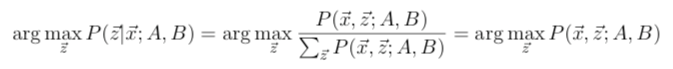
更快的做法同样是动态规划。和前向算法不同的地方在于，使用最大化操作代替求和操作，即Viterbi算法。也就是说，现在是跟踪最大化见过的观测子序列的概率，而不是前向算法是对见过的观测子序列的概率全部求和。

3）学习问题：已知观测序列x，求转移矩阵A、发射矩阵B - Baum-Welch算法（前向-后向算法）

可以理解x是一个很长的序列，和通常的监督学习问题不同在于并非是批量的label-feature样本。

状态序列是隐变量序列。根据EM算法，E步找一个下界逼近目标函数，M步调整参数最大化这个下界：

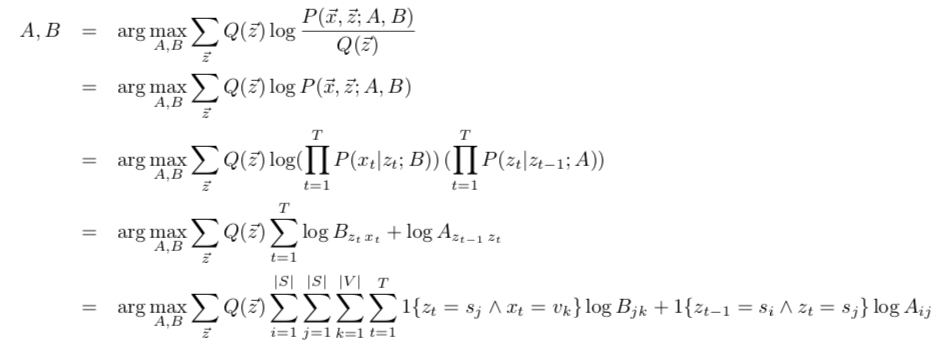
转化为Lagrange multipliers：

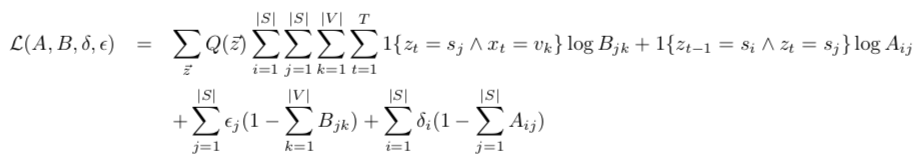
分别对参数求偏导并令其为零：

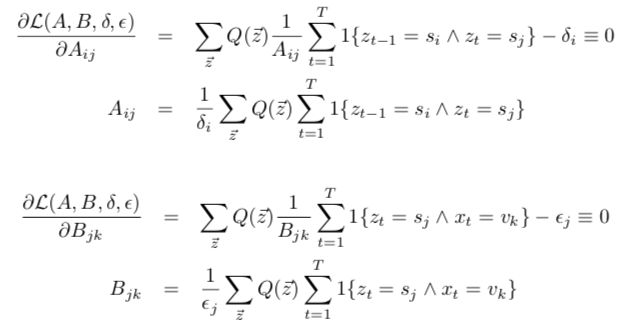
代入得到参数A，B的估计：

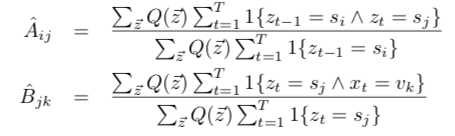
对A的分子部分使用bayes定理并用前向算法和后向算法转化：

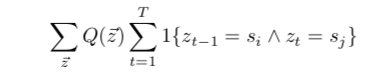
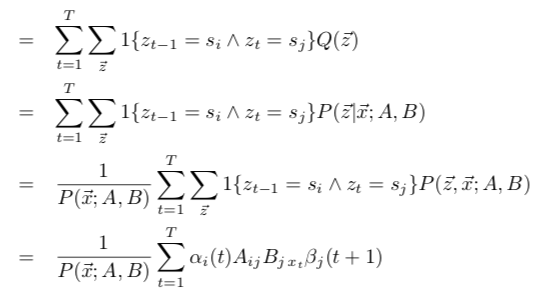
A的分母部分类似：

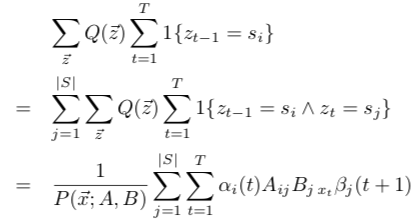
综合得到A的估计：

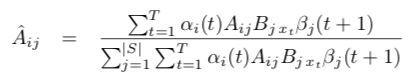
同理得到B的估计：

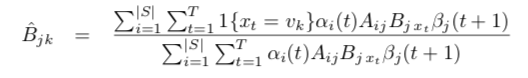
实际计算中直接计算充分统计量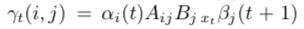 

和通常的EM求解的问题类似，也是非凸问题，容易陷入局部极值。因此需要做不同的初始化运行多次算法。另外，对于没有样本覆盖到A、B的转移或发射概率的实际问题，需要做平滑操作。