2015 省赛 简单的图论问题? bfs

• [E] 简单的图论问题?

• 时间限制: 5000 ms　内存限制: 65535 K
• 问题描述

• 给一个 n 行 m 列的迷宫,每个格子要么是障碍物要么是空地。每个空地里都有一个权值。你的 任务是从找一条(r1,c1)到(r2,c2)的路径,使得经过的空地的权值之和最小。每一步可以往上下 左右四个方向之一移动一格,但不能斜着移动,也不能移动到迷宫外面或者进入障碍物格子。

  如下图,灰色格子代表障碍物。路径 A->B->D->F->E 的权值为 10+3+6+14+8=41,它是从 A 到 E 的最优路径。注意,如果同一个格子被经过两次,则权值也要加两次。

  

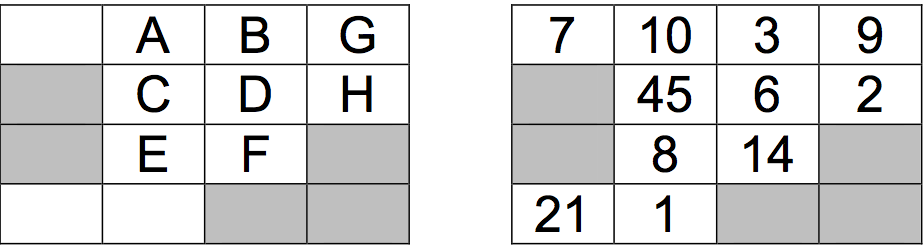
  为了让题目更有趣(顺便增加一下难度),你还需要回答另外一个问题:如果你每次必须转弯 (左转、右转或者后退,只要不是沿着上次的方向继续走即可),最小权值是多少?比如,在 上图中,如果你刚刚从 A 走到 B,那么下一步你可以走到 D 或者 A,但不能走到 G。在上图 中,A 到 E 的最优路径是 A->B->D->H->D->F->E,权和为 10+3+6+2+6+14+8=49。注意,D 经 过了两次。

• 输入
• 输入包含不超过 10 组数据。每组数据第一行包含 6 个整数 n, m, r1, c1, r2, c2 (2<=n,m<=500, 1<=r1,r2<=n, 1<=c1,c2<=m). 接下来的 n 行每行包含 m 个格子的描述。每个格子要么是一个 1~100 的整数,要么是星号"*"(表示障碍物)。起点和终点保证不是障碍物。
• 输出
• 对于每组数据,输出两个整数。第一个整数是“正常问题”的答案,第二个整数是“有趣问 题”的答案。如果每个问题的答案是“无解”,对应的答案应输出-1。
• 样例输入

• 4 4 1 2 3 2
  7 10 3 9

  * 45 6 2

  * 8 14 *
  
21 1 * *
  2 4 1 1 1 4
  1 2 3 4
  9 * * 9
  2 4 1 1 1 4
  1 * 3 4
  9 9 * 9 

• 样例输出

• Case 1: 41 49
  Case 2: 10 -1
  Case 3: -1 -1

• 提示

• 无

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<queue>
using namespace std;
#define maxn 510
int n,m,xs,ys,xe,ye;
int dx[]={,-,,},dy[]={,,,-};
int mapn[maxn][maxn];
int vis[maxn][maxn],vis2[maxn][maxn][];
struct node{
    int x,y,step,dir;
    friend bool operator<(node a, node b) {return a.step>b.step;}
};
int bfs(){
    node p;
    p.x = xs,p.y = ys,p.step = mapn[xs][ys];
    priority_queue<node> q;
    q.push(p);
    vis[xs][ys] = ;
    while(!q.empty()){
        node now = q.top();
        q.pop();
        for(int i=;i<;i++){
            int xx = now.x + dx[i];
            int yy = now.y + dy[i];
            if(xx>=&&xx<n&&yy>=&&yy<m&&
            mapn[xx][yy]!=-&&!vis[xx][yy]){
                vis[xx][yy] = ;
                node tmp;
                tmp.x = xx;
                tmp.y = yy;
                tmp.step = now.step + mapn[xx][yy];
                if(now.x == xe && now.y == ye){
                        cout << now.step << " ";
                       return ;
                   }
                q.push(tmp);
            }
        }
    }
    return ;
}
int bfs2(){//有趣的情况
    node p;
    p.x = xs,p.y = ys,p.step = mapn[xs][ys],p.dir=-;
    priority_queue<node> q;
    q.push(p);
    while(!q.empty()){
        node now = q.top();
        q.pop();
        for(int i=;i<;i++){
            int xx = now.x + dx[i];
            int yy = now.y + dy[i];
            if(xx>=&&xx<n&&yy>=&&yy<m&&now.dir!=i&&
            mapn[xx][yy]!=-&&!vis2[xx][yy][i]){
                vis2[xx][yy][i] = ;//vis2为三维数组，多存了一个方向
                node tmp;
                tmp.x = xx;
                tmp.y = yy;
                tmp.step = now.step + mapn[xx][yy];
                tmp.dir = i;//dir为当前方向
                if(now.x == xe && now.y == ye){
                        cout << now.step << endl;
                       return ;
                   }
                q.push(tmp);
            }
        }
    }
    return ;
}
int main()
{
    char ch[];
    int num,t=;
    while(cin >> n >> m >> xs >> ys >> xe >> ye){
        t++;
        memset(vis2,,sizeof(vis2));
        memset(vis,,sizeof(vis));
        xs--,ys--,xe--,ye--;
        getchar();
        for(int i=;i<n;i++){
            int l = ;
            gets(ch);
            int len = strlen(ch);
            for(int j=;j<len;j++){
            //注意这种同时处理字符和数字的情况，这里数字从题目那里知道是小于或等于三位数
                if(ch[j] == '*'){
                    mapn[i][l] = -;
                    l++;
                }
                else if(ch[j]>=''&&ch[j]<=''){
                    num = ch[j]-'';
                    if(ch[j+]>=''&&ch[j+]<=''){
                        num = num*+(ch[j+]-'');
                        j++;
                        if(ch[j+]>=''&&ch[j+]<=''){
                            num = num*+(ch[j+]-'');
                            j++;
                        }
                    }
                    mapn[i][l]=num;
                    l++;
                }
            }
        }
        printf("Case %d: ",t);
        if(bfs() == ){
            cout << "-1 ";
        }
        if(bfs2() == ){
            cout << "-1" << endl;
        }
    }
    return ;
}