CF981C Useful Decomposition 树 dfs 二十三 *

Useful Decomposition

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Ramesses knows a lot about problems involving trees (undirected connected graphs without cycles)!

He created a new useful tree decomposition, but he does not know how to construct it, so he asked you for help!

The decomposition is the splitting the edges of the tree in some simple paths in such a way that each two paths have at least one common vertex. Each edge of the tree should be in exactly one path.

Help Remesses, find such a decomposition of the tree or derermine that there is no such decomposition.

Input

The first line contains a single integer nn (2≤n≤1052≤n≤105) the number of nodes in the tree.

Each of the next n−1n − 1 lines contains two integers aiai and bibi (1≤ai,bi≤n1≤ai,bi≤n, ai≠biai≠bi) — the edges of the tree. It is guaranteed that the given edges form a tree.

Output

If there are no decompositions, print the only line containing "No".

Otherwise in the first line print "Yes", and in the second line print the number of paths in the decomposition mm.

Each of the next mm lines should contain two integers uiui, vivi (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi) denoting that one of the paths in the decomposition is the simple path between nodes uiui and vivi.

Each pair of paths in the decomposition should have at least one common vertex, and each edge of the tree should be presented in exactly one path. You can print the paths and the ends of each path in arbitrary order.

If there are multiple decompositions, print any.

Examples

input

Copy

4
1 2
2 3
3 4

output

Copy

Yes
1
1 4

input

Copy

6
1 2
2 3
3 4
2 5
3 6

output

Copy

No

input

Copy

5
1 2
1 3
1 4
1 5

output

Copy

Yes
4
1 2
1 3
1 4
1 5

Note

The tree from the first example is shown on the picture below: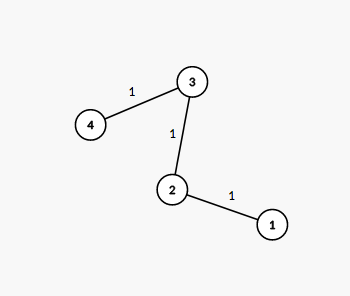The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

The tree from the second example is shown on the picture below: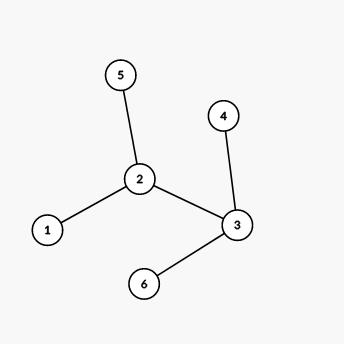We can show that there are no valid decompositions of this tree.

The tree from the third example is shown on the picture below: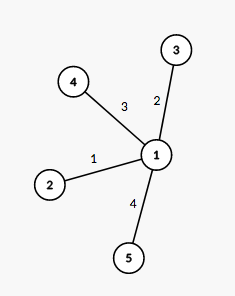The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

 题意： 问在1-n之间是否有一个个点可以一次走完全部的点

 题解：当度数大于等于3的点最多只有一个时可以遍历，否则不行。一次dfs找出以那个点为根节点的所有叶子节点（配合vector遍历）

 

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
#define debug(a) cout << #a << " " << a << endl
using namespace std;
const int maxn = 1e5 + ;
const int mod = 1e9 + ;
typedef long long ll;
ll n, u, v, vis[maxn];
vector<ll> V[maxn], ans;
struct node {
    ll num, val;
}deg[maxn];
bool cmp( node a, node b ) {
    return a.num > b.num;
}
void dfs( ll k, ll last ) {
    vis[k] = ;
    if( V[k].size() ==  && V[k][] == last ) {
        ans.push_back(k);
        return ;
    }
    for( ll i = ; i < V[k].size(); i ++ ) {
        if( !vis[V[k][i]] ) {
            dfs( V[k][i], k ) ;
        }
    }
    return ;
}
int main(){
    std::ios::sync_with_stdio(false);
    cin >> n;
    memset( vis, , sizeof(vis) );
    for( ll i = ; i <= n; i ++ ) {
        deg[i].val = i;
    }
    for( ll i = ; i < n; i ++ ) {
        cin >> u >> v;
        deg[u].num ++, deg[v].num ++;
        V[u].push_back(v), V[v].push_back(u);
    }
    sort( deg+, deg+n+, cmp );
    if( deg[].num >=  ) {
        cout << "No" << endl;
    } else {
        cout << "Yes" << endl;
        dfs( deg[].val, -1e9 );
        cout << ans.size() << endl;
        for( ll i = ; i < ans.size(); i ++ ) {
            cout << deg[].val << " " << ans[i] << endl;
        }
    }
    return ;
}