AVL树的左旋右旋理解 (转)
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
AVL树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL旋转"。
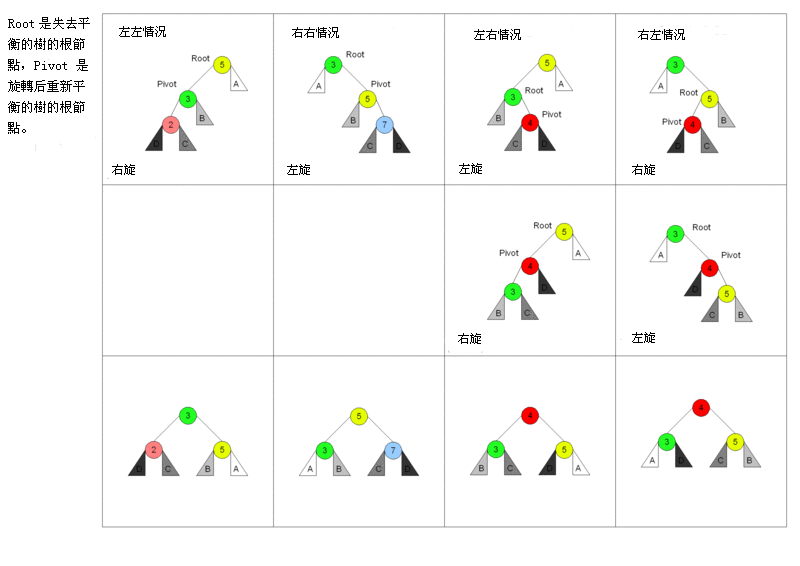
以上内容转自维基百科AVL树
从图中可以比较形象的看出所谓左旋右旋的旋转支点是三个主节点中大小居中的那个节点,左旋就是左边的节点降下来,右旋就是右边的节点降下来,都成为中间节点的子树。
左右双旋分解就是先将左侧节点降为左子树,右边节点将为右子树。当然中间有合并子树的过程,这里没有细说。
高度为h的AVL树,节点数N最多 ; 最少
; 最少 ( 其中
( 其中 )N是h的斐波那契数列。
)N是h的斐波那契数列。
AVL树的左旋右旋理解 (转)的更多相关文章
- 高级数据结构---红黑树及其插入左旋右旋代码java实现
前面我们说到的二叉查找树,可以看到根结点是初始化之后就是固定了的,后续插入的数如果都比它大,或者都比它小,那么这个时候它就退化成了链表了,查询的时间复杂度就变成了O(n),而不是理想中O(logn), ...
- delphi 图像处理 图像左旋右旋
procedure TDR_QM_ZP_Form.btn_ZXClick(Sender: TObject); //图像左旋 begin screen.Cursor := crhourglass; my ...
- 对于AVL树和红黑树的理解
AVL又称(严格)高度平衡的二叉搜索树,也叫二叉查找树.平衡二叉树.window对进程地址空间的管理用到了AVL树. 红黑树是非严格平衡二叉树,统计性能要好于平衡二叉树.广泛的在C++的STL中,ma ...
- 数据结构与算法(九):AVL树详细讲解
数据结构与算法(一):基础简介 数据结构与算法(二):基于数组的实现ArrayList源码彻底分析 数据结构与算法(三):基于链表的实现LinkedList源码彻底分析 数据结构与算法(四):基于哈希 ...
- AVL树的理解及自写AVL树
AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下都是O(log n).增加和删除可能需要通过一次或多 ...
- 单例模式,堆,BST,AVL树,红黑树
单例模式 第一种(懒汉,线程不安全): public class Singleton { private static Singleton instance; private Singleton () ...
- AVL树(二叉平衡树)详解与实现
AVL树概念 前面学习二叉查找树和二叉树的各种遍历,但是其查找效率不稳定(斜树),而二叉平衡树的用途更多.查找相比稳定很多.(欢迎关注数据结构专栏) AVL树是带有平衡条件的二叉查找树.这个平衡条件必 ...
- python常用算法(5)——树,二叉树与AVL树
1,树 树是一种非常重要的非线性数据结构,直观的看,它是数据元素(在树中称为节点)按分支关系组织起来的结构,很像自然界中树那样.树结构在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可用树形 ...
- 数据结构之平衡二叉树(AVL树)
平衡二叉树(AVL树)定义如下:平衡二叉树或者是一棵空树,或者是具有以下性质的二叉排序树: (1)它的左子树和右子树的高度之差绝对值不超过1: (2)它的左子树和右子树都是平衡二叉树. AVL树避免了 ...
随机推荐
- 易买网(注册Ajax讲解)
关于注册(用到Ajax) 运用onblur进行时时刷新 创建所需用的Servlet 好了 Ajax其实不是很难 如果还是不懂可以私信我呦-^^-!
- linux根目录详解
ubuntu 文件说明:http://tech.ccidnet.com/art/302/20080118/1347213_1.html/ 根目录 | |-boot/ 启动文件.所有与系统启动有关的 ...
- JS选择checkbox
<script> window.onload = function () { //获取checkbox var ids1 = document.getElementsByName('Vot ...
- php访问控制
访问控制 访问控制通过关键字public,protected和private来实现.被定义为公有的类成员可以在任何地方被访问.被定义为受保护的类成员则可以被其自身以及其子类和父类访问.被定义为私有的类 ...
- Leetcode 解题 Median of Two sorted arrays
题目:there are two sorted arrays nums1 and nums2 of size m and n respectively. Find the median of the ...
- NDK_ROOT找不到的解决方法 MACOS
只要在Eclipse上进行配置就行了,看图说话
- ubuntu apt-get常用命令的使用
packagename指代为软件包的名称 apt-get install packagename 安装一个新软件包(参见下文的aptitude) apt-get remove ...
- 配置Apache服务器 数据库mySQL
Mac 配置 apache php 详细解说 一.开启apache 并切改变引导 1.打开终端 输入:sudo apachectl start 回车,关闭终端 2.打开浏览器,地址栏输入 ...
- PHP中的urlencode和urldecode的理解
平时在工作中经常要写 $xxx = urldecode($_GET['xxx']);的类似代码,大部分的情况都是没有问题的.也能很好的工作. 所以也没有怎么在意.但是突然有一天我想到 $xxx =$_ ...
- Android中JNI编程的那些事儿(1)
转:Android中JNI编程的那些事儿(1)http://mobile.51cto.com/android-267538.htm Android系统不允许一个纯粹使用C/C++的程序出现,它要求必须 ...
