P5024 保卫王国[倍增+dp]

窝当然不会ddp啦，要写这题当然是考虑优化裸dp啦，但是这题非常麻烦，于是变成了黑题。

首先，这个是没有上司的舞会模型，求图的带权最大独立集。

不考虑国王的限制条件，有

\[dp[x][0]+=dp[y][1]\\
dp[x][1]+=min(dp[y][1],dp[y][0])
\]

现在考虑限制条件，如果对每一个限制条件都做一次dp，复杂度达到\(O(n^2)\)，无法承受。

显然，对于这些限制条件，每一次的变动不会影响其它大多数的状态。

对于一个限制条件，我们分开考虑，先考虑只对一个城市进行限制的情况。

若该城市被要求驻扎军队，那么如果在最优情况下它本来就需要军队，则没有影响；如果它本来不需要军队，由于此时所有子树都是最优解，那么它只会对从它到根节点的路径的最优解产生影响。

若该城市被要求不能驻扎，那么与上面的情况类似，如果它本来需要驻扎，那么会对它到根节点的路径造成影响。

综上所述，我们是否可以考虑对于每个限制条件，只对两个点到根节点之间的路径的某些状态进行修改呢？答案是肯定的。

假设待修改节点为\(x\)。首先，此时除了\(x\sim root\)的路径上的节点所表示的状态，其它状态都是最优的。对于这条路径的更新，实际上就是又对这条路径做了一次dp，并强制\(x\)选或不选，从而限制转移。

显然这是可行的，但是复杂度仍为\(O(n^2)\)，我们需要一些手段进行优化。

容易发现我们更新的是一条链，对于一条链，我们自然可以想到用倍增或者树剖（它们维护的都是树链）来处理每个点的转移。

以倍增为例。

首先考虑裸dp的步骤，一个一个跳，每次从儿子转移。那我们能不能一段一段地跳，每次从已有信息中转移呢？当然可以。

先考虑只有一个点的情况。

如果我们要对\(x\)进行限制，那么我们不妨把整个图变成这样，方便分析

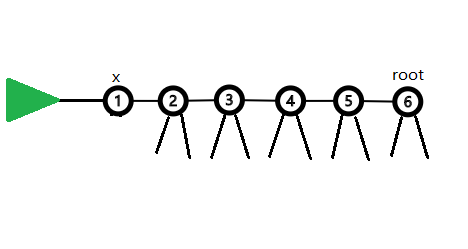
其中绿色的部分是\(x\)的子树的最优解。

显然我们在修改一个点之后，造成的对原最优解的影响是一定的，产生的新最优解是一定的，这意味着我们可以通过一些手段预处理出来。

不妨考虑通过倍增预处理出最优情况下每个点产生变动（选变成不选，不选变成选）在这条\(x\sim root\)的链上产生的新最优解，也就是预处理出修改后dp时跳某一段的该段最优解。

然后从\(x\)树上倍增跳到\(root\)，合并所得的新的最优解，就是这次限制条件下的答案。

实际上，我们的倍增预处理是在一次裸dp的基础上进行的。换句话说，倍增时用到的信息就是每个点表示的状态的原来的最优解，然后加一个限制条件，再做一个dp。

形象的讲，这个倍增预处理，就是dp套dp。

那这个倍增怎么做呢？

考虑状态的刻画，显然由几个较小的子问题合并成较大的子问题时，这些较小的子问题不能有交叉，否则无法基于二进制划分合并成更大的子问题。再者，子问题必须覆盖整个状态空间。也就是说，在状态定义时，我们要不重不漏。

既然如此，对于第一点，不难想到倍增时我们不仅要记录\(x\)的状态（0/1），还要记录它跳\(2^k\)步的祖先的状态。

对于第二点，不难想出状态包含的范围。

设\(f[0/1][0/1][k][x]\)表示\(x\)节点变为0不可选、1可选时，向上\(2^k\)步的祖先\(y\)为0可选、1不可选时，\(y\)除去\(x\)以及\(x\)的子树的原最优解的其它所有子树的新最优解。

如下图，假设节点3是\(x\)的\(2^k\)祖先，状态为红色部分

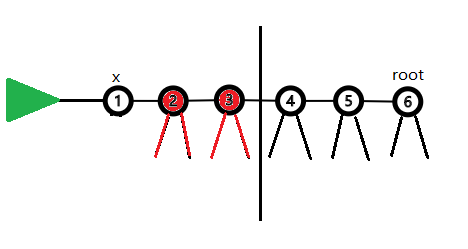
而3的\(2^k\)祖先（假设是\(root\)）表示的状态就是蓝色部分。

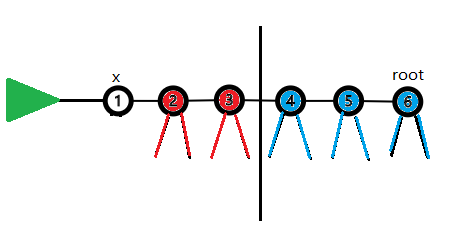
这样就可以很好的合并状态，之后统计答案的过程中，我们只需枚举\(x\)的状态并倍增跳即可。

对于节点\(y\)，它的父节点为\(x\)，有

\[f[1][0][0][y]=dp[0][x]-dp[1][y]\\ f[0][1][0][y]=f[1][1][0][y]=dp[1][x]-min(dp[1][y],dp[0][y])
\]

得到转移（cao）

\[f[0][0][j][y]=min(f[0][0][j-1][y]+f[0][0][j-1][fa],f[0][1][j-1][y]+f[1][0][j-1][fa])\\
f[0][1][j][y]=min(f[0][0][j-1][y]+f[0][1][j-1][fa],f[0][1][j-1][y]+f[1][1][j-1][fa])\\
f[1][0][j][y]=min(f[1][0][j-1][y]+f[0][0][j-1][fa],f[1][1][j-1][y]+f[1][0][j-1][fa])\\
f[1][1][j][y]=min(f[1][0][j-1][y]+f[0][1][j-1][fa],f[1][1][j-1][y]+f[1][1][j-1][fa])
\]

然后就是统计答案，当然是倍增统计答案。

从待修改点的两种不同状态开始往上倍增合并新最优解，直到根节点。

对于两个待修改点\(x,y\)的情况，我们像求LCA一样，先统计\(x\sim lca(x,y),y\sim lca(x,y)\)，再统计\(lca(x,y)\sim root\)即可。

注意一个细节，当\(x,y\)两点跳到\(lca\)的儿子处我们需要同时减去它们两个的原最优解，再往上跳。

复杂度降至\(O(nlogn)\)。

树剖也是一个道理，预处理变动后最优解。

参考代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 100010
#define MOD 2520
#define E 1e-12
#define ll long long
using namespace std;
inline ll read()
{
	ll f=1,x=0;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;
}
struct rec{
	int next,ver;
}g[N<<1];
int head[N],tot,n,m;
ll dp[2][N],f[2][2][21][N],gi[21][N],t,dep[N],w[N];
inline void add(int x,int y)
{
	g[++tot].ver=y;
	g[tot].next=head[x],head[x]=tot;
}
inline void dfs(int x,int fa)
{
	dp[1][x]=w[x];dep[x]=dep[fa]+1;
	f[0][0][0][x]=INF,gi[0][x]=fa;
	for(int j=1;j<t;++j) gi[j][x]=gi[j-1][gi[j-1][x]];
	for(int i=head[x];i;i=g[i].next){
		int y=g[i].ver;
		if(y==fa) continue;
		dfs(y,x);
		dp[0][x]+=dp[1][y];
		dp[1][x]+=min(dp[1][y],dp[0][y]);
	}
}
inline void init()
{
	queue<ll> q;
	q.push(1);
	f[1][0][0][1]=dp[0][0]-dp[1][1];
	f[0][1][0][1]=f[1][1][0][1]=dp[1][0]-min(dp[1][1],dp[0][1]);
	while(q.size()){
		ll x=q.front();q.pop();
		for(int i=head[x];i;i=g[i].next){
			int y=g[i].ver;
			if(y==gi[0][x]) continue;
			f[1][0][0][y]=dp[0][x]-dp[1][y];
			f[0][1][0][y]=f[1][1][0][y]=dp[1][x]-min(dp[1][y],dp[0][y]);
			for(int j=1;j<t;++j){
				int fa=gi[j-1][y];
				f[0][0][j][y]=min(f[0][0][j-1][y]+f[0][0][j-1][fa],f[0][1][j-1][y]+f[1][0][j-1][fa]);
				f[0][1][j][y]=min(f[0][0][j-1][y]+f[0][1][j-1][fa],f[0][1][j-1][y]+f[1][1][j-1][fa]);
				f[1][0][j][y]=min(f[1][0][j-1][y]+f[0][0][j-1][fa],f[1][1][j-1][y]+f[1][0][j-1][fa]);
				f[1][1][j][y]=min(f[1][0][j-1][y]+f[0][1][j-1][fa],f[1][1][j-1][y]+f[1][1][j-1][fa]);
			}
			q.push(y);
		}
	}
}
inline ll get(ll x,int a,ll y,int b)
{
	ll ans=0,lca;
	if(dep[x]<dep[y]) swap(x,y),swap(a,b);
	ll x0=INF,x1=INF,y0=INF,y1=INF,l0=INF,l1=INF;
	a?x1=dp[1][x]:x0=dp[0][x],b?y1=dp[1][y]:y0=dp[0][y];
	for(int j=t;j>=0;--j){
		ll t0=x0,t1=x1;
		if(dep[gi[j][x]]>=dep[y]){
			x0=min(t0+f[0][0][j][x],t1+f[1][0][j][x]);
			x1=min(t0+f[0][1][j][x],t1+f[1][1][j][x]);
			x=gi[j][x];
		}
	}
	if(x==y) lca=x,b?l1=x1:l0=x0;
	else {
		for(int j=t;j>=0;--j){
			if(gi[j][x]!=gi[j][y]){
				ll t0=x0,t1=x1,p0=y0,p1=y1;
				x0=min(t0+f[0][0][j][x],t1+f[1][0][j][x]);
				x1=min(t0+f[0][1][j][x],t1+f[1][1][j][x]);
				y0=min(p0+f[0][0][j][y],p1+f[1][0][j][y]);
				y1=min(p0+f[0][1][j][y],p1+f[1][1][j][y]);
				x=gi[j][x],y=gi[j][y];
			}
		}
		lca=gi[0][x];
		l0=dp[0][lca]-dp[1][x]-dp[1][y]+x1+y1;
		l1=dp[1][lca]-min(dp[0][x],dp[1][x])-min(dp[0][y],dp[1][y])+min(x1,x0)+min(y1,y0);
	}
	if(lca==1) ans=min(l0,l1);
	else{
		for(int j=t;j>=0;--j){
			if(dep[gi[j][lca]]>1){
				ll t0=l0,t1=l1;
				l0=min(t0+f[0][0][j][lca],t1+f[1][0][j][lca]);
				l1=min(t0+f[0][1][j][lca],t1+f[1][1][j][lca]);
				lca=gi[j][lca];
			}
		}
		ans=min(dp[0][1]-dp[1][lca]+l1,dp[1][1]-min(dp[0][lca],dp[1][lca])+min(l1,l0));
	}
	return ans<INF?ans:-1;
}
int main()
{
	n=read(),m=read();
	char op[5];
	cin>>op;
	t=log2(n)+1;
	for(int i=1;i<=n;++i) w[i]=read();
	for(int i=1;i<n;++i){
		ll u=read(),v=read();
		add(u,v),add(v,u);
	}
	dfs(1,0);
	init();
	while(m--){
		ll x=read(),a=read(),y=read(),b=read();
		if(a==0&&b==0&&(gi[0][x]==y||gi[0][y]==x)){
			puts("-1");continue;
		}
		printf("%lld\n",get(x,a,y,b));
	}
	return 0;
}