特征的非线性变换（Feature Non-linear Transformation）

有时候特征x和目标y不呈线性关系，线性模型y=wx+b不能很好地反映事物的规律或者无法对事物进行有效分类，因此此时我们需要使用非线性模型。

（x=([x₁,x₂,...,x_n])^T，w=([w₁,w₂,...,w_n])^T）

比如说下图的分类问题，显然无论用什么样的直线都很难把圈圈和叉叉很好地分隔开来，但是用一个大圆圈却能很好地进行分隔。

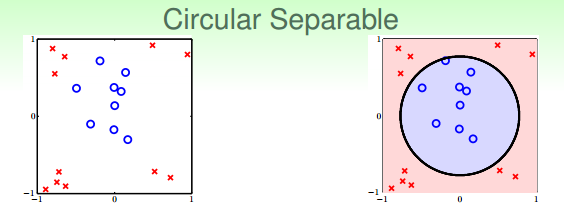
这个大圆圈就是使用了非线性模型拟合的结果，以往线性模型中的分类超平面（这里是直线）变成了圆：−x₁²​−x₂²​+0.6=0。

可以看到，此时假设函数的特征不是线性模型的(x₁，x₂)，而是变成了(x₁^2，x₂^2)。我们通过映射关系z=x²，就可以把特征变为(z₁，z₂)。此时就相当于把x域中的二次式转换为z域中的一次式，得到线性组合。

我们把x_n​→z_n​这个转换过程称之为特征变换（Feature Transform）（这里是非线性变换）。通过特征的非线性变换，可以将非线性模型转换为另一个域中的线性模型来求解。具体过程如下：把原始x值通过映射关系转换成z值，数据由(x_n​,y_n)变为(z_n​,y_n)；在z域中用线性算法对转换后的数据进行训练，得到最佳w值；训练好线性模型之后，再将z替换为x的映射关系。

需要注意的是：特征变换只是得到新特征的一种方式，可以和任何线性模型结合使用。将线性模型变为非线性模型，并不需要改变模型本身，只需要改变特征输入即可。比如原本线性模型有一个特征x₁，其有两个输入值：

[[2]
 [3]]

变换为二次模型（quadratic model）后，新的特征输入就变为：

[[4]
 [9]]

上面的例子是将原始特征x转变为二次式x²，也可以将x转变为其他形式，例如：可以将特征x变为log(x)，exp(x)，x^0.5，sin(x)，cos(x)，等等。

下面再来说一下结构化的变换方式：多项式变换（Polynomial Transformation）。

如果原本的特征x是2维的，即有2个特征：(x₁，x_2​)，那么它的二次多项式为：(x₁，x₂，x₁^2，x₁x₂，x₂^2，1)，一共有6项。

如果原本的特征x是d维的，即有d个特征：(x₁，x₂，…，x_d)，那么做一个完全的二次变换（其包含所有的二次项、一次项和常数项，此时得到非线性组合：C*d^1+C*d^2+1）后得到的特征维度是：d(d+3)​/2+1。

 

如果变换的阶数更高呢？推广上面的结论，假设阶数为Q，那么对于d维的特征x，将其变换为Q次多项式后，对应的z域的特征维度大约为：。

由上图可以看到，将特征x进行多项式变换后，计算和储存新特征的时间复杂度和空间复杂度是O(Q^d)---Q的d次方。随着Q和d的增大，计算量和储存量都会变得很大。这就是线性模型变为多项式非线性模型所要付出的代价。

另一个所要付出的代价则更严重，那就是模型复杂度会变高（假设空间的VC维近似等于特征的个数）。我们知道，模型复杂度越高，我们所需要的训练数据也就越多，否则将很容易发生过拟合现象。因此，应先从阶数低的变换开始做起，以防止过拟合问题的发生。

附注：如果特征输入值很小，那么应变换为勒让德多项式（Legendre polynomials）。