边缘检测sobel算子

sobel算子 - sophia_hxw - 博客园http://www.cnblogs.com/sophia-hxw/p/6088035.html

#1，个人理解

网上查了很多资料，都说sobel算子是用来检测边缘的，分别给了两个方向上的卷积核，然后说明做法，就说这就是sobel算子。对于我个人来说，还有很多不明白的地方，所以理清下思路。

#2，边缘、边界和sobel算子

这个可以自己去google或者百度找定义，边缘和边界不一样，两者没有必然联系也并非毫无联系。因为现实世界的三维空间映射到图像显示的二维空间中会丢失很多信息，也会添进来一部分类似光照、场景等的干扰，所以并不能完全给边缘和边界的关系下一个定义。对图像而言，我们一般是要找出它的边缘，因为这是图像处理中使用较多的一个特征。何为边缘？图像处理中认为，灰度值变化剧烈的地方就是边缘。那么如何判断灰度值变化？如何度量“剧烈”？sobel算子就对这些问题做了自己的规范，而且命名为sobel算子，就是对一副图像的输入到输出边缘信息的整个处理过程。

sobel算子的思想，Sobel算子认为，邻域的像素对当前像素产生的影响不是等价的，所以距离不同的像素具有不同的权值，对算子结果产生的影响也不同。一般来说，距离越远，产生的影响越小。

sobel算子的原理，对传进来的图像像素做卷积，卷积的实质是在求梯度值，或者说给了一个加权平均，其中权值就是所谓的卷积核；然后对生成的新像素灰度值做阈值运算，以此来确定边缘信息。

#3，卷积核及计算方法

若Gx是对原图x方向上的卷积，Gy是对原图y方向上的卷积；

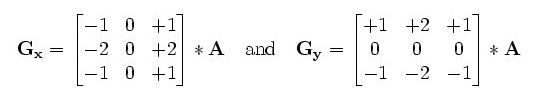
原图中的作用点像素值通过卷积之后为：

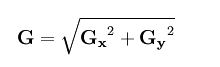
可以简化成：

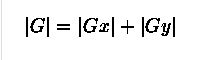
比如，一下矩阵为原图中的像素点矩阵，带入上式中的A，最终得到的G或者|G|是下面(x,y)处的像素值，可以自己去搜索下卷积的含义来理解。

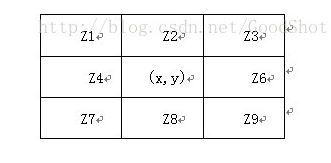
另外，卷积核也可以旋转，用与查找不与x,y轴平行或垂直的方向上的边缘。

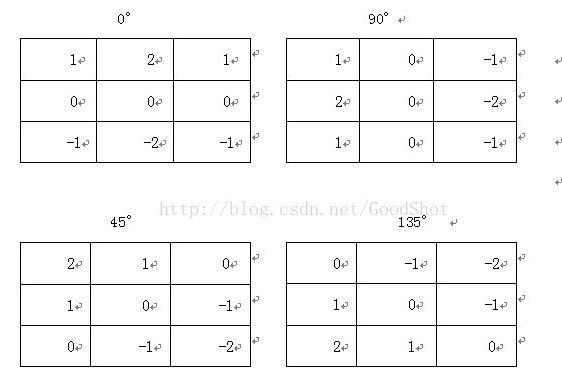
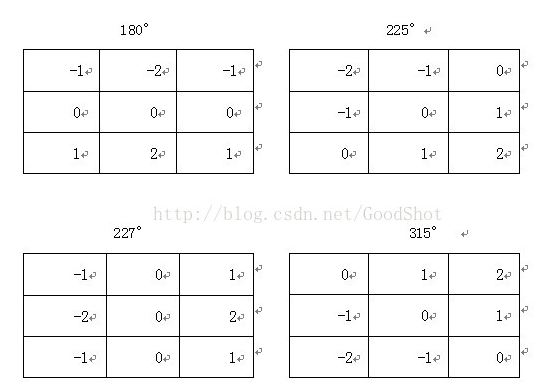
#4，阈值处理及平滑处理

得到像素点新的像素值之后，给定一个阈值就可以得到sobel算子计算出的图像边缘了。

通常，为了消除噪声对sobel算子的影响，会增加一个预处理的操作，主要是做平滑处理降低噪声的影响。

#5，matlab代码实现

Gx=[1.0 2.0 1.0;0.0 0.0 0.0;-1.0 -2.0 -1.0];

Gy=[-1.0 0.0 1.0;-2.0 0.0 2.0;-1.0 0.0 1.0];

img=imread('qiaoba.jpg');

image=rgb2gray(img);

subplot(2,2,1);

imshow(image);

title('原图');

gradx=conv2(Gx,image,'full');

gradx=abs(gradx); %计算图像的sobel垂直梯度

subplot(2,2,2);

imshow(gradx,[]);

title('图像的sobel垂直梯度');

grady=conv2(Gy,image,'full');

grady=abs(grady); %计算图像的sobel水平梯度

subplot(2,2,3);

imshow(grady,[]);

title('图像的sobel水平梯度');

grad=gradx+grady; %得到图像的sobel梯度

subplot(2,2,4);

imshow(grad,[]);

title('图像的sobel梯度');

处理结果：

#5，c++代码实现

来源：http://blog.csdn.net/dcrmg/article/details/52280768

#include "core/core.hpp"

#include "highgui/highgui.hpp"

#include "imgproc/imgproc.hpp"

#include "iostream"

using namespace std;

using namespace cv;

int main(int argc, char *argv[])

{

Mat image = imread("qiaoba.jpg", 0);

Mat imageX = Mat::zeros(image.size(), CV_16SC1);

Mat imageY = Mat::zeros(image.size(), CV_16SC1);

Mat imageXY = Mat::zeros(image.size(), CV_16SC1);

Mat imageX8UC;

Mat imageY8UC;

Mat imageXY8UC;

if (!image.data)

{

return -1;

}

GaussianBlur(image, image, Size(3, 3), 0); //高斯滤波消除噪点

uchar *P = image.data;

uchar *PX = imageX.data;

uchar *PY = imageY.data;

int step = image.step;

int stepXY = imageX.step;

for (int i = 1; i<image.rows - 1; i++)

{

for (int j = 1; j<image.cols - 1; j++)

{

//通过指针遍历图像上每一个像素

PX[i*imageX.step + j*(stepXY / step)] = abs

(P[(i - 1)*step + j + 1] + P[i*step + j + 1] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[i*step + j - 1] * 2 - P[(i + 1)*step + j - 1]);

PY[i*imageX.step + j*(stepXY / step)] = abs

(P[(i + 1)*step + j - 1] + P[(i + 1)*step + j] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[(i - 1)*step + j] * 2 - P[(i - 1)*step + j + 1]);

}

addWeighted(imageX, 0.5, imageY, 0.5, 0, imageXY);//融合X、Y方向

convertScaleAbs(imageX, imageX8UC);

convertScaleAbs(imageY, imageY8UC);

convertScaleAbs(imageXY, imageXY8UC); //转换为8bit图像

Mat imageSobel;

Sobel(image, imageSobel, CV_8UC1, 1, 1); //Opencv的Sobel函数

imshow("Source Image", image);

imshow("X Direction", imageX8UC);

imshow("Y Direction", imageY8UC);

imshow("XY Direction", imageXY8UC);

imshow("Opencv Soble", imageSobel);

waitKey();

return 0;

}

#6,sobel算子的优缺点

优点：计算简单，速度很快；

缺点：计算方向单一，对复杂纹理的情况显得乏力；

　　直接用阈值来判断边缘点欠合理解释，会造成较多的噪声点误判。