数学：Burnside引理与Pólya定理

这个计数定理在考虑对称的计数中非常有用

先给出这个定理的描述，虽然看不太懂：

在一个置换群G={a1,a2,a3……ak}中，把每个置换都写成不相交循环的乘积。 

设C1(ak)是在置换ak的作用下不动点的个数，也就是长度为1的循环的个数。通过上述置换的变换操作后可以相等的元素属于同一个等价类

那么等价类的个数就等于：

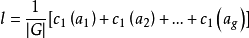
然后理解一下公式

一正方形分成4格，2着色，有多少种方案？其中，经过转动相同的图象算同一方案。

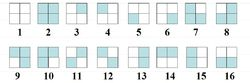
关于转动，一共有四种置换方法，也就是｜G｜=4

不动(360度)：a1=(1)(2)…(16)
逆时针转90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)
顺时针转90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)
转180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)

然后我们针对每一种置换的方式，找到其中的不动点，也就是只有自己的情况

由Burnside引理，共有(16+2+2+4)/4=6(种方案)

然后的Pólya定理其实就是简化这个运算用的

利用Burnside引理要首先列出所有n^m种可能的染色方案，然后找出在每个置换下保持不变的方案数。

然后找出在每个置换下保持不变的方案数,显然当m或n很大的时候,复杂度会炸

Polya定理实际上是Burnside引理的具体化，提供了计算不动点的具体方法

假设一个置换有σk个循环,就是轮换

易知每个循环对应的所有位置颜色需一致，而任意两个循环之间选什么颜色互不影响。

因此，如果有m种可选颜色，则该置换对应的不动点个数为m^σk。

用其替换Burnside引理中的C(G)，即C(G)=m^k。得到等价类数目为：

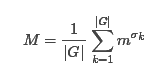
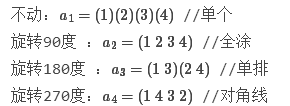
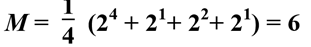
老实说，我看不懂这个怎么用的。。

burnside定理就是 非等价染色数 = 在G中单个置换下保持不变的染色数的平均数

而polya定理说的是一种特殊情况，若有m中颜色，每种颜色不限数量，则在G中的某个置换g下，保持不变的染色数=m^k，k为置换g的循环个数

典型例题POJ1286

我们需要求的也就是不同置换的个数，和每一个置换的循环节数

旋转，旋转i个小球的距离，那么会得到0～n-1的置换方案，共有n种，对于旋转i个小球的循环节数为gcd(n,i)

翻转，对于偶数，不经过小球有对称抽有n/2个，每种置换方案有n/2+1个循环节；经过小球的对称轴有n/2个，每种置换方案有n/2个循环节

对于奇数，经过小球的对称轴，有n个，每种方案有n/2+1个循环节

 #include<cstdio>
 long long n,ans;
 long long gcd(long long a,long long b)
 {
     return b==?a:gcd(b,a%b);
 }
 long long pow(long long x,long long k)
 {
     if(k==) return x;
     long long s=pow(x,k/);
     s=s*s;
     if(k%) s*=x;
     return s;
 }
 int main()
 {
     while(scanf("%lld",&n)==&&n!=-)
     {
         if(n==)
         {
             printf("0\n");
             continue;
         }
         ans=;
         for(int i=;i<n;i++)
             ans+=pow(,gcd(n,i));
         if(n%)
         {
             ans+=n*pow(,n/+);
         }
         else
         {
             ans+=n/*pow(,n/);
             ans+=n/*pow(,n/+);
         }
         printf("%lld\n",ans/(n*));
     }
     return ;
 }