题解 CF191C 【Fools and Roads】

树上差分半裸题

常规思路是进行三次DFS，然后常规运算即可

这里提供两次dfs的思路（wyz tql orz）

我们以样例2为例

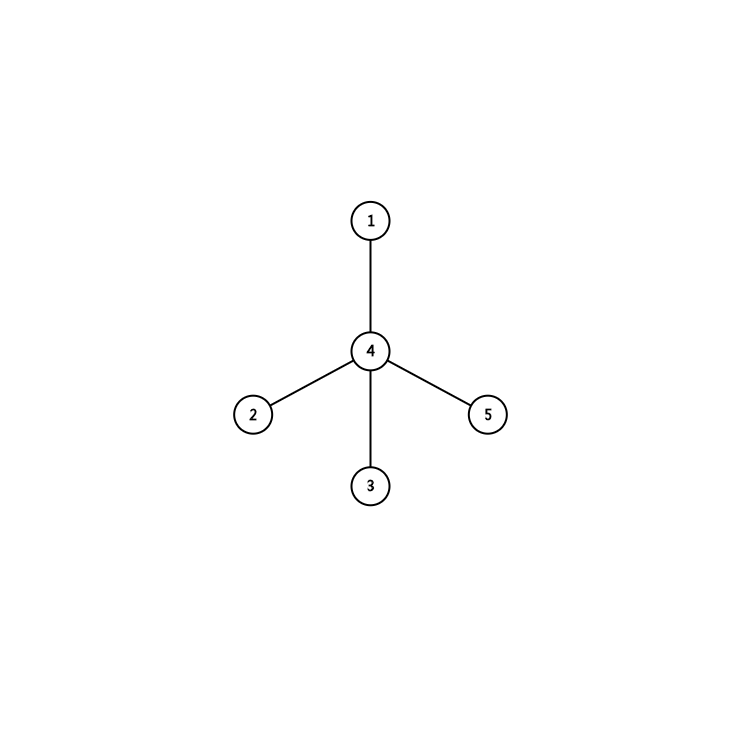
我们考虑任意一条路径，令其起点为u终点为v，每走一次当前路径则v的访问次数必定+1，于是我们可以使每一个点表示连接其上的一条边的访问次数，所以我们令节点v的访问次数+1;

与此同时，过程中的路径也同样会被访问，且这里是双向边，于是与此同时的我们也令节点u的访问次数+1;当然访问当前子树下根节点中包含的两个点并不会访问，而我们在增加u和v的访问时同时也错误地增加了其公共父节点的访问量，于是我们令lca(u,v)的访问量-2即可。

例如上图中我们从节点5走到节点3，我们令节点3与节点5的访问次数+1，同时使节点4的访问次数-2。

如下：

while(k--){
    int u=read(),v=read();
    diff[u]++,diff[v]++,diff[lca(u,v)]-=2;
}

最后输出答案时只需要判断每条边两端点的深度大小即可。

#include<bits/stdc++.h>
#define int long long
#define maxn 100005
using namespace std;
inline char get(){
    static char buf[30000],*p1=buf,*p2=buf;
    return p1==p2 && (p2=(p1=buf)+fread(buf,1,30000,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
    register char c=get();register int f=1,_=0;
    while(c>'9' || c<'0')f=(c=='-')?-1:1,c=get();
    while(c<='9' && c>='0')_=(_<<3)+(_<<1)+(c^48),c=get();
    return _*f;
}
struct edge{
    int u,v,w,next;
    int num=0;
}E[maxn<<1];
int n,k;
int p[maxn],eid;
int d[maxn], parent[maxn][20];
int diff[maxn];
inline void init(){
    for(register int i=0;i<maxn;i++)p[i]=d[i]=-1;
    eid=0;
}
inline void insert(int u,int v){
    E[eid].u=u;
    E[eid].v=v;
    E[eid].next=p[u];
    p[u]=eid++;
}
inline void insert2(int u,int v){
    insert(u,v);
    insert(v,u);
}
void dfs(int u){
    for (register int i=p[u];~i;i=E[i].next) {
        if (d[E[i].v]==-1){
            d[E[i].v]=d[u]+1;
            parent[E[i].v][0]=u;
            dfs(E[i].v);
        }
    }
}
int lca(int x, int y) {
    int i,j;
    if(d[x]<d[y])swap(x,y);
    for(i=0;(1<<i)<=d[x];i++);
    i--;
    for(register int j=i;j>=0;j--){
        if (d[x]-(1<<j)>=d[y])x=parent[x][j];
    }
    if(x==y)return x;
    for(register int j=i;j>=0;j--){
        if(parent[x][j]!=parent[y][j]) {
            x=parent[x][j];
            y=parent[y][j];
    	}
    }
    return parent[x][0];
}
int dd[maxn];
void dfs_(int u,int fa,int flag){
	dd[u]=flag;
    for(register int i=p[u];~i;i=E[i].next){
        int v=E[i].v;
        if(fa==v)continue;
        dfs_(v,u,flag+1);
        diff[u]+=diff[v];
    }
}
int u[maxn],v[maxn];
signed main(){
    //freopen("1.txt","r",stdin);
    init();
    n=read();
    for(register int i=2;i<=n;i++){
        u[i]=read(),v[i]=read();
        insert2(u[i],v[i]);
    }
    d[1]=0;
    dfs(1);
    for(register int level=1;(1<<level)<=n;level++){
        for(register int i=1;i<=n;i++){
            parent[i][level]=parent[parent[i][level-1]][level-1];
        }
    }
    k=read();
    while(k--){
        int casu=read(),casv=read();
        diff[casu]++,diff[casv]++,diff[lca(casu,casv)]-=2;
    }
    dfs_(1,-1,1);
    for(register int i=2;i<=n;i++){
    	if(dd[u[i]]>=dd[v[i]])cout<<diff[u[i]]<<" ";
    	else cout<<diff[v[i]]<<" ";
	}
    return 0;
}