Softmax回归(Softmax Regression, K分类问题)
- Softmax回归:K分类问题, 2分类的logistic回归的推广。其概率表示为:
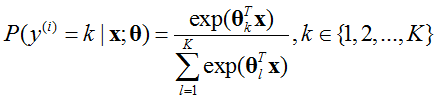
对于一般训练集:
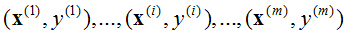
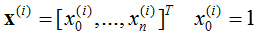
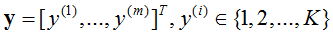
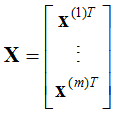
系统参数为:
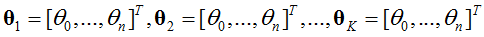
- Softmax回归与Logistic回归的关系
当Softmax回归用于2分类问题,那么可以得到:
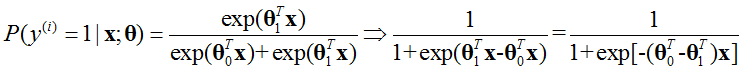
令θ=θ0-θ1,就得到了logistic回归。所以实际上logistic回归虽然有2个参数向量,但这2个参数向量可以退化到1个参数向量。推广到K个类别,那么就需要K-1个参数向量
- 参数求解
类似于logistic regression,求最大似然概率,有:
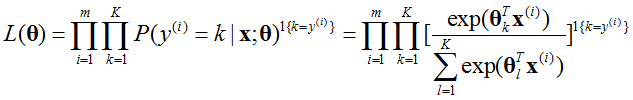
其中1{k=y}为真值表达式,例如如果1{1+1=2},那么值为1,如果1{1+1=0},那么值为0。对数似然函数有:
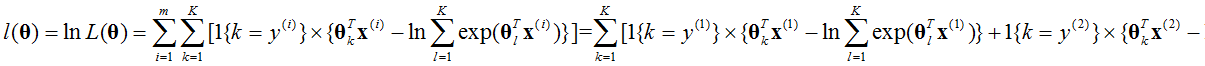
上式中,仅有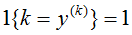 ,所以有:
,所以有:
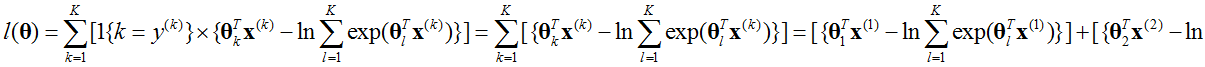
对上式求导数
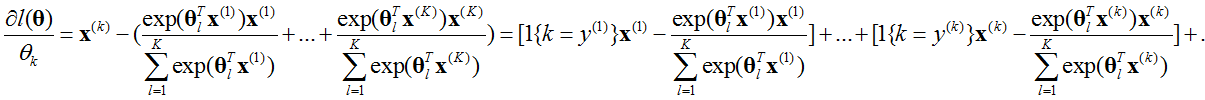
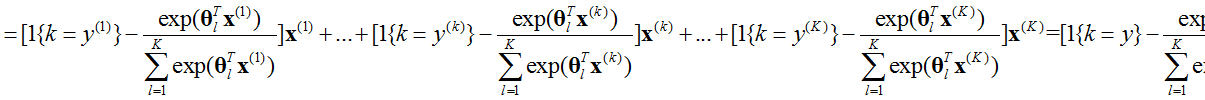
Softmax回归(Softmax Regression, K分类问题)的更多相关文章
- Softmax回归 softMax回归与logistic回归的关系
简介 在本节中,我们介绍Softmax回归模型,该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签 可以取两个以上的值. Softmax回归模型对于诸如MNIST手写数字分 ...
- 《转》Logistic回归 多分类问题的推广算法--Softmax回归
转自http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92 简介 在本节中,我们介绍Softmax回归模型,该模型是log ...
- 逻辑回归,多分类推广算法softmax回归中
转自http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92 简介 在本节中,我们介绍Softmax回归模型,该模型是log ...
- 【机器学习】Softmax 和Logistic Regression回归Sigmod
二分类问题Sigmod 在 logistic 回归中,我们的训练集由 个已标记的样本构成: ,其中输入特征.(我们对符号的约定如下:特征向量 的维度为 ,其中 对应截距项 .) 由于 logis ...
- 《动手学深度学习》系列笔记—— 1.2 Softmax回归与分类模型
目录 softmax的基本概念 交叉熵损失函数 模型训练和预测 获取Fashion-MNIST训练集和读取数据 get dataset softmax从零开始的实现 获取训练集数据和测试集数据 模型参 ...
- Machine Learning 学习笔记 (3) —— 泊松回归与Softmax回归
本系列文章允许转载,转载请保留全文! [请先阅读][说明&总目录]http://www.cnblogs.com/tbcaaa8/p/4415055.html 1. 泊松回归 (Poisson ...
- Softmax回归
Reference: http://ufldl.stanford.edu/wiki/index.php/Softmax_regression http://deeplearning.net/tutor ...
- 机器学习 —— 基础整理(五)线性回归;二项Logistic回归;Softmax回归及其梯度推导;广义线性模型
本文简单整理了以下内容: (一)线性回归 (二)二分类:二项Logistic回归 (三)多分类:Softmax回归 (四)广义线性模型 闲话:二项Logistic回归是我去年入门机器学习时学的第一个模 ...
- logistic回归和softmax回归
logistic回归 在 logistic 回归中,我们的训练集由 个已标记的样本构成:.由于 logistic 回归是针对二分类问题的,因此类标记 . 假设函数(hypothesis functi ...
随机推荐
- [android] 天气app布局练习(三)
主要练习LinearLayout和layout_weight属性 <RelativeLayout xmlns:android="http://schemas.android.com/a ...
- log4j的简单使用
引入jar包org.apache.log4j.Logger,项目src目录下建立一个log4j.properties配置文件 log4j.rootLogger=INFO,A1,R log4j.appe ...
- 1.JDBC基础
JDBC全称Java Database Connectivity,即Java数据库连接.(以下以MySQL为例,使用MySQL语句) Sun公司提供了标准JDBC API接口,没有实现具体类.各个数据 ...
- lintcode 刷题记录··
单例模式,用C#实现过单例模式,python区别就是类里边的静态方法写法不一样,python叫类方法,函数之前加@classmethod class Solution: # @return: The ...
- jsp实现html页面静态化
一.实现原因 1.网站访问量过大,导致服务器压力加大以及数据库数据交换频繁.生成静态页面提供访问以缓解压力. 2.静态页面是动态页面的备份,若动态页面出现异常,静态页面可以暂时替代. 二.使用场合 ...
- 使用mpvue搭建一个初始小程序
1. 初始化一个 mpvue 项目 现代前端开发框架和环境都是需要 Node.js 的,如果没有的话,请先下载 nodejs 并安装. 然后打开命令行工具: # 1. 先检查下 Node.js 是否安 ...
- ImportError: No module named bs4错误解决方法
前言:毕业论文打算用Python做爬虫爬一些数据,最近开始入门Python: 在学习的时候遇到一个问题,按照看的文章安装了Python,也配置了相应的环境(使用window系统),使用pycharm编 ...
- Centos 7 系统安装(简单步骤)
前面步骤忽略.进入安装步骤. 运行安装 到选择语言的时候最好选英文版,这里做模板,用的中文版 接着下一步到安装选项 在日期和时间里,选择上海时区 紧接着进行软件安装选择,如图安装就好 接着进行分区,也 ...
- null id in com.rocky.** entry 错误处理
1. 概述 使用hibernate往mysql数据库插入记录出错如下 10:37:57,364 ERROR [AssertionFailure] an assertion failure occure ...
- Java的异常处理throw和throws的区别
区别一: throw 是语句抛出一个异常:throws 是方法抛出一个异常: throw语法:throw <异常对象> ...
