Deep Learning基础--线性解码器、卷积、池化

本文主要是学习下Linear Decoder已经在大图片中经常采用的技术convolution和pooling，分别参考网页http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial中对应的章节部分。

　　Linear Decoders:

　　以三层的稀疏编码神经网络而言，在sparse autoencoder中的输出层满足下面的公式：

　　

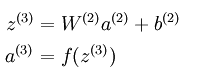
　　从公式中可以看出，a3的输出值是f函数的输出，而在普通的sparse autoencoder中f函数一般为sigmoid函数，所以其输出值的范围为(0,1)，所以可以知道a3的输出值范围也在0到1之间。另外我们知道，在稀疏模型中的输出层应该是尽量和输入层特征相同，也就是说a3=x1，这样就可以推导出x1也是在0和1之间，那就是要求我们对输入到网络中的数据要先变换到0和1之间，这一条件虽然在有些领域满足，比如前面实验中的MINIST数字识别。但是有些领域，比如说使用了PCA Whitening后的数据，其范围却不一定在0和1之间。因此Linear Decoder方法就出现了。Linear Decoder是指在隐含层采用的激发函数是sigmoid函数，而在输出层的激发函数采用的是线性函数，比如说最特别的线性函数——等值函数。此时，也就是说输出层满足下面公式：

　　

　　这样在用ＢＰ算法进行梯度的求解时，只需要更改误差点的计算公式而已，改成如下公式：

　　

　　

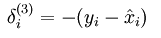
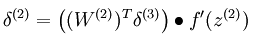
　　Convolution:

　　在了解convolution前，先认识下为什么要从全部连接网络发展到局部连接网络。在全局连接网络中，如果我们的图像很大，比如说为96*96，隐含层有要学习100个特征，则这时候把输入层的所有点都与隐含层节点连接，则需要学习10^6个参数，这样的话在使用BP算法时速度就明显慢了很多。

　　所以后面就发展到了局部连接网络，也就是说每个隐含层的节点只与一部分连续的输入点连接。这样的好处是模拟了人大脑皮层中视觉皮层不同位置只对局部区域有响应。局部连接网络在神经网络中的实现使用convolution的方法。它在神经网络中的理论基础是对于自然图像来说，因为它们具有稳定性，即图像中某个部分的统计特征和其它部位的相似，因此我们学习到的某个部位的特征也同样适用于其它部位。

　　下面具体看一个例子是怎样实现convolution的，假如对一张大图片Xlarge的数据集，r*c大小，则首先需要对这个数据集随机采样大小为a*b的小图片，然后用这些小图片patch进行学习（比如说sparse autoencoder），此时的隐含节点为k个。因此最终学习到的特征数为：

　　

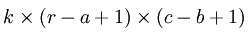
　　此时的convolution移动是有重叠的。

　　Pooling：

　　虽然按照convolution的方法可以减小不少需要训练的网络参数，比如说96*96，,100个隐含层的，采用8*8patch，也100个隐含层，则其需要训练的参数个数减小到了10^3，大大的减小特征提取过程的困难。但是此时同样出现了一个问题，即它的输出向量的维数变得很大，本来完全连接的网络输出只有100维的，现在的网络输出为89*89*100=792100维，大大的变大了，这对后面的分类器的设计同样带来了困难，所以pooling方法就出现了。

　　为什么pooling的方法可以工作呢？首先在前面的使用convolution时是利用了图像的stationarity特征，即不同部位的图像的统计特征是相同的，那么在使用convolution对图片中的某个局部部位计算时，得到的一个向量应该是对这个图像局部的一个特征，既然图像有stationarity特征，那么对这个得到的特征向量进行统计计算的话，所有的图像局部块应该也都能得到相似的结果。对convolution得到的结果进行统计计算过程就叫做pooling，由此可见pooling也是有效的。常见的pooling方法有max pooling和average pooling等。并且学习到的特征具有旋转不变性（这个原因暂时没能理解清楚）。

　　从上面的介绍可以简单的知道，convolution是为了解决前面无监督特征提取学习计算复杂度的问题，而pooling方法是为了后面有监督特征分类器学习的，也是为了减小需要训练的系统参数（当然这是在普遍例子中的理解，也就是说我们采用无监督的方法提取目标的特征，而采用有监督的方法来训练分类器）。

　　参考资料：

http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial

http://www.cnblogs.com/tornadomeet/archive/2013/03/25/2980766.html