BZOJ2005:[NOI2010]能量采集(莫比乌斯反演,欧拉函数)

Description

栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。 栋栋的植物种得非常整齐，一共有n列，每列有m棵，植物的横竖间距都一样，因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1至n，表示是在第x列，y的范围是1至m，表示是在第x列的第y棵。 由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是(0, 0)。 能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能量的损失为2k + 1。例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于连接线段上存在一棵植物(1, 2)，会产生3的能量损失。注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。现在要计算总的能量损失。 下面给出了一个能量采集的例子，其中n = 5，m = 4，一共有20棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。 在这个例子中，总共产生了36的能量损失。

Input

仅包含一行，为两个整数n和m。

Output

仅包含一个整数，表示总共产生的能量损失。

Sample Input

【样例输入1】
5 4
【样例输入2】
3 4

Sample Output

【样例输出1】
36
【样例输出2】
20
对于100%的数据：1 ≤ n, m ≤ 100,000。

Solution

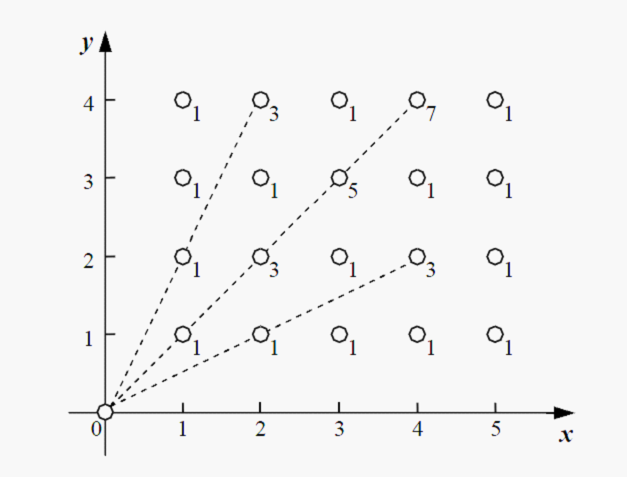
首先要知道一点，就是对于一个点$(x,y)$来说，ta到起点的连线会经过$gcd(x,y)-1$个点（不包含本身）为什么我也不会证，不过感性理解非常正确

所以题目就成了求$\sum_{i=1}^{n}\sum_{j=1}^{m}2*(gcd(i,j)-1)+1$

化简一下就成了$2*\sum_{i=1}^{n}\sum_{j=1}^{m}gcd(i,j)-n*m$

也就是求出$\sum_{i=1}^{n}\sum_{j=1}^{m}gcd(i,j)$题目就结束了 。

以下假设n<m

$\sum_{i=1}^n \sum_{j=1}^mgcd(i,j)$

$=\sum_{p=1}^{n} p \sum_{i=1}^n \sum_{j=1}^m[gcd(i,j)=p]$

$=\sum_{p=1}^np\sum_{i=1}^{\left \lfloor \frac{n}{p} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{p} \right \rfloor}[gcd(i,j)=1]$

$=\sum_{p=1}^np\sum_{i=1}^{\left \lfloor \frac{n}{p} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{p} \right \rfloor}\sum_{d|gcd(a,b)}\mu(d)$

$=\sum_{p=1}^np\sum_{d=1}^{\left \lfloor \frac{n}{p} \right \rfloor}\mu(d){\left \lfloor \frac{n}{pd} \right \rfloor}{\left \lfloor \frac{m}{pd} \right \rfloor}$

设$pd=T$

$=\sum_{T=1}^{n}{\left \lfloor \frac{n}{T} \right \rfloor}{\left \lfloor \frac{m}{T} \right \rfloor}\sum_{p|T}p*\mu(\frac{T}{p})$

$=\sum_{T=1}^{n}{\left \lfloor \frac{n}{T} \right \rfloor}{\left \lfloor \frac{m}{T} \right \rfloor}φ(T)$

$\sum_{p|T}p*\mu(\frac{T}{p})=φ(T)$好像是因为用到了求欧拉函数的时候容斥的思想QAQ……

Code

 #include<iostream>
 #include<cstdio>
 #define N (100000)
 using namespace std;

 long long ans,n,m,sum[N+],phi[N+];

 void Get_phi()
 {
     phi[]=;
     for (int i=; i<=N; ++i)
         if (!phi[i])
             for (int j=i; j<=N; j+=i)
             {
                 if (!phi[j]) phi[j]=j;
                 phi[j]=phi[j]/i*(i-);
             }
     for (int i=; i<=N; ++i) sum[i]=sum[i-]+phi[i];
 }

 int main()
 {
     scanf("%lld%lld",&n,&m);
     if (n>m) swap(n,m);
     Get_phi();
     for (int l=,r; l<=n; l=r+)
     {
         r=min(n/(n/l),m/(m/l));
         ans+=(sum[r]-sum[l-])*(n/l)*(m/l);
     }
     printf("%lld\n",*ans-n*m);
 }