信号分析——从傅里叶变化到FFT

我们眼中的世界就像皮影戏的大幕布，幕布的后面有无数的齿轮，大齿轮带动小齿轮，小齿轮再带动更小的。

在最外面的小齿轮上有一个小人——那就是我们自己。

我们只看到这个小人毫无规律的在幕布前表演，却无法预测他下一步会去哪。

而幕布后面的齿轮却永远一直那样不停的旋转，永不停歇。

——这就是对傅里叶世界观的描述。

你眼中看似落叶纷飞变化无常的世界，实际只是躺在上帝怀中一份早已谱好的乐章。

下面进入正式环节↓↓↓↓↓↓

---

傅里叶公式：

其中：

这就是鼎鼎大名的傅里叶公式！

简单的理解：

每一个信号，在某个特定的配方下，都可以由简单的正弦曲线组成。傅里叶男爵猜测任意周期函数都可以写成三角函数之和。具体需要多少呢？无数个！【嘿， 上帝才不会让你这么简单的就发现他】

（插入题外话：为什么是男爵呢？傅里叶大佬曾经跟着拿破仑混过）

傅里叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

 深入理解看这里：https://www.matongxue.com/madocs/619.html

 

为什么信号分析采用傅里叶变换？

时域信号在经过傅立叶变换的分解之后，变为了不同正弦波信号的叠加，我们再去分析这些正弦波的频率，可以将一个信号变换到频域。

有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。【时域频域下面就讲到了啦

---

如果通过表示

根据欧拉公式【欧拉公式的意义就是旋转啦】，有：

　　　　　　　　　

一个可以观察到旋转的频率，所以称为频域（Frequency domain）；一个可以看到流逝的时间，所以称为时域（time domain）。

动图在这里！：https://en.wikipedia.org/wiki/File:Fourier_series_square_wave_circles_animation.gif

所以时域、频域到底是啥？

时域

信号时域分析就是分析信号随时间的变化，比如24 小时体温监测图即体温随时间变化。

时域分析反映在图象上最明显的特征就是横轴以时间为变量，纵轴因描述的变量不同而不同。

记住横轴是时间就好啦！

频域

频率就是指单位时间内发生的次数，一般用 F 来表示。

日常生活中我们经常接触到一些频率的描述，比如听收音机时，要调频选台，其中调频，就是要调至某一频率；我们家用的电器上也经常标着 220V ，50Hz，而50Hz就是指频率为50赫兹。

频域分析反映在图象上自变量是频率,即横轴是频率,纵轴是该频率信号的幅度。

实际上频域和时域只是人们对信号分析的不同方法。 好啦， 脑子里记住两个坐标吧。

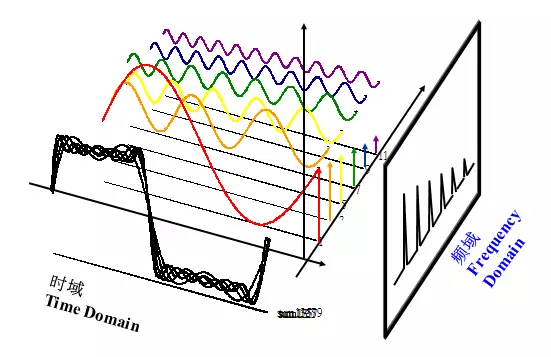
总的来说这就是他们的面貌啦， 下面继续深入。

---

时域转化为频域

首先的问题是为什么要转？

如图， 将时域信号经过一种非常有用的数学变换一傅里叶变换（1），就可转化到频域，得到信号的频谱 ，这就是频谱分析；

反过来 ，我们也可将频域信号通过逆傅里叶变换（2）转换成时域信号。

由时域变换到频域，我们也可以分析信号中包含的各种频率分量的幅值、功率、能量和相位关系，也就是分析信号的频谱特性。

既然通过信号的频域分析，可以知道信号含各个频率的成分多少，我们就可以设计滤波器的频率来抑制某些信号而放大另一些我们感兴趣的信号。

例如：噪音属于高频区域，将时域转换成频域， 在频域中去掉噪音所属的高频区， 再转换回来， 就可以去掉噪音了。

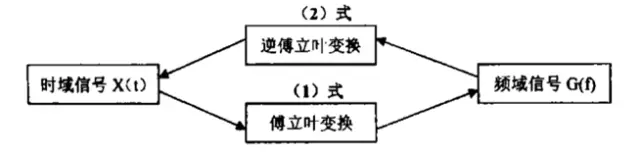
下面这张图立马看懂啦！！！

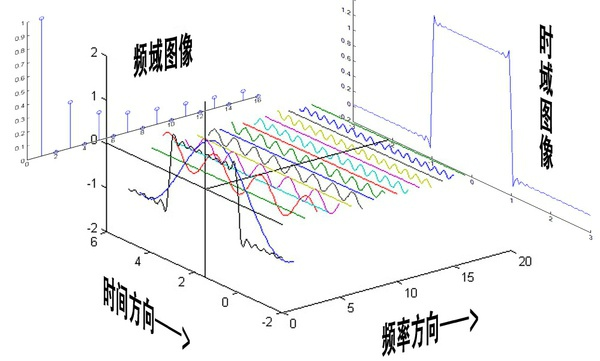
动图在这里！：https://en.wikipedia.org/wiki/File:Fourier_series_and_transform.gif

---

好啦， 下面可以讲FFT啦。

FFT是何方神圣？

FFT是离散傅立叶变换（DFT）的快速算法，可以将一个信号变换到频域。

首先介绍DFT（离散傅里叶变化）：

【一大波公式即将来袭~~~不要怕， 挺好理解的， 看不懂也不怎么影响理解。】

对于点序列，它的离散傅里叶变换（DFT）为

其中是自然对数的底数，是虚数单位。

理解成矩阵变化吧。

这个式子很显然复杂度是O(N*N)

为啥要FFT？因为fast呀！

---

FFT（快速傅里叶变换）

FFT推导如下：

单位根：

在复平面上，以原点为圆心， 1为半径作圆，所得的圆叫做单位圆。

以原点为起点，单位圆的 n 等分点为终点，作 n 个向量。设所得的幅角为正且最小的向量对应的复数为 ω_n ，称为 n 次单位根。

ω_n为单位根 

对每一个ω_n：

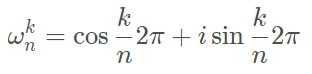
单位根的性质

证明：

• 
• 它们表示的点（或向量）表示的复数是相同的

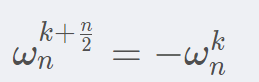
证明：

• 
• 它们表示的点关于原点对称，所表示的复数实部相反，所表示的向量等大反向

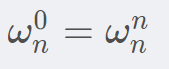
都等于1

最常用的 FFT 算法 —— Cooley-Tukey 算法。

设一个多项式A(x)

对比两个式子

现在我们就可以递归分治来搞FFT了

每一次回溯时只扫当前前面一半的序列，即可得出后面一半序列的答案

私聊：hichens@qq.com