#Week4 Logistic Regression

一、Classification

主要讨论二元分类。

线性回归处理分类问题显然不靠谱，所以采用逻辑回归。

二、Hypothesis Representation

假设函数变为\(h_\theta(x)=g(\theta^TX)\)，使得分类器的输出在[0,1]之间。

\(g(z)=\frac{1}{1+e^{-z}}\)，叫做sigmoid函数:



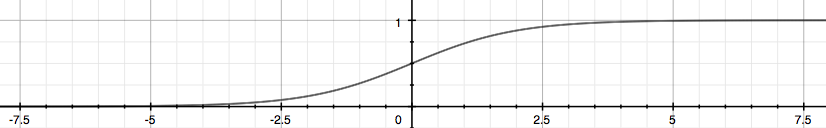
这个算出的值代表\(y\)是正向类的概率。

三、Decision Boundary

将阈值设为0.5，那么可以得知：当\(\theta^TX>=0\)时，预测\(y\)为1，否则为0。

Decision Boundary就是分隔\(y=1\)与\(y=0\)的边界，这个边界可以是任何形状，取决于假设函数。

上图：



效果非常好，那么如果训练集的数据不是这么规则呢？

四、Cost Function

将逻辑回归的代价函数定义为：





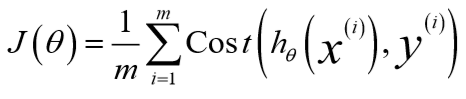
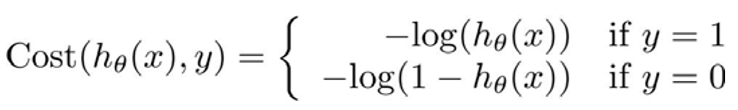
如果沿用线性回归的cost function，那么得到的\(J(\theta)\)是非凸的，这样不利于寻找全局最优解。

如果预测值\(h_\theta(x)=1\)，实际的标签\(y\)也是1，那么\(cost=0\)；

如果预测值\(h_\theta(x)=0\)，而实际的标签\(y\)是1，那么\(cost=+\infin\)，可以看作是对算法预测错误的惩罚。。。

同样的，\(y=0\)也具有相似的特征。

简化上述代价函数：



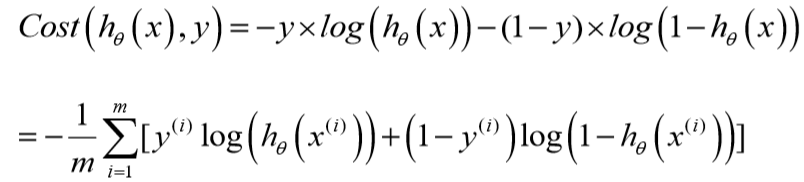
所以cost function的向量化表示：

\[h = g(X\theta)
\]

\[J(\theta) = \frac{1}{m} \cdot \left(-y^{T}\log(h)-(1-y)^{T}\log(1-h)\right)
\]

可以通过求出\(J(\theta)\)的最小值，得出参数\(\theta\)，接着用\(h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}\)得到我们的预测值。

怎么求出\(J(\theta)\)的最小值呢？对了，就是Gradient Descent.



向量化表示：



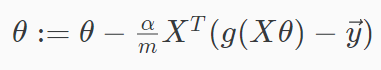
这个和之前线性回归更新参数的公式是一样的，但是由于\(h_\theta(x)\)不同，所以这两个梯度下降是完全不同的。

五、Multiclass classification

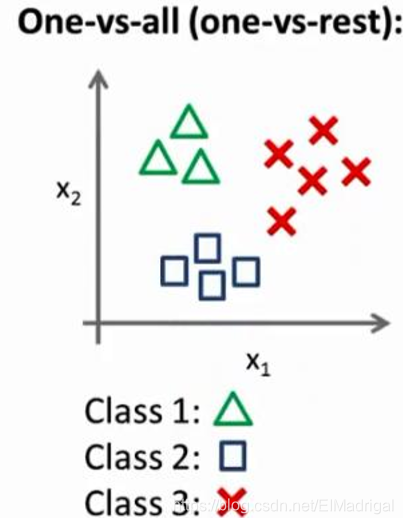
将其中的一个类作为正向类(y=1)，其余作为负向类，分别训练出很多分类器，最后选择令输出值\(h_\theta^{i}(x)\)最大的一个\(i\)作为预测值。

相当于每一个分类器都可以识别一种类别：