python C3算法

Python MRO

C3算法是python当中计算类继承顺序的一个算法，从python2.3以后就一直使用此算法了。

c3 linearization算法称为c3线性化算法

C3算法原理

首先定义几个符号的意义：

符号	意义
L	针对一个类进行解析用L进行表示，例如L(A)表示对类A进行解析
merge	合并操作的一个函数（后面具体介绍）
C	表示一个类名
B	表示是C的一个子类，如果多个子类用B1，B2....表示
+	元素列表顺序添加
tail	去除列表第一个元素，例如 tail([1,2,3,4]) = [2,3,4]

L(C) = C + merge(L(B1) + L(B2) + ...+ )

merge函数合并规则：

1. 首先选中merge 函数的第一个参数(也是一个列表)，按照公式里的描述就是L(B1)。
2. 取列表中第一个元素记为h，如果h没有出现其他 列表的tail中， 那么将其移到 merge函数前，提取出来，并且将这个元素在所有列表中移除，并重复 2。
3. 如果出现在其他列表中的 tail 中，寻找下一个列表。
4. merge 函数所有元素都被移除类创建成功，如果寻找不到下一个列表则创建失败。

下面举例说明：

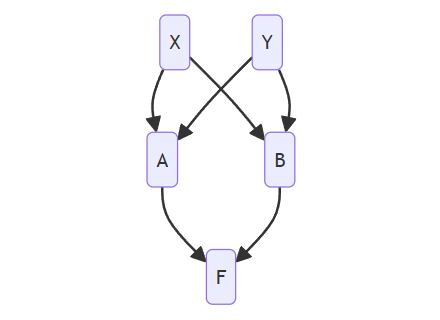
class X():
    pass

class Y():
    pass

class A(X, Y):
    pass

class B(X, Y):
     pass

class F(A, B):
    pass
print(F.__mro__)

我们来解析 F的mro顺序，则首先记为 L(F)，根据

L(C) = C + merge(L(B1) + L(B2) + ...+ )

公式得到:

L(F) = F + merge(L(A)+L(B))

接下来计算L(A)，与L(B):

L(A) = A + merge(L(X),L(Y)) = A + merge([X],[Y]) = [A,X,Y]
L(B) = B + merge(L(X),L(Y)) = B + merge([X],[Y]) = [B,X,Y]

带入 L(F) = L(F) + merge(L(A)+L(B)) 得到：

L(F) = F + merge([A,X,Y],[B,X,Y])

下面是关键merge逻辑理解了，首先根据 merge 的说明 1，选中得到 [A,X,Y], 根据merge的说明2，选中第一个元素 A， 判断A 是否在 tail(B,X,Y) 中，即 A 是否在 [X，Y] 中，不在，将其提出来，得到：

L(F) = F + merge([A,X,Y],[B,X,Y]) = [F,A] + merge([X,Y],[B,X,Y])

接着重复 merge的2，判断 X 是否在 tail(B,X,Y)=[X,Y] 中，结果是存在，那么寻找[X，Y]的下一个列表，即[B,X,Y]，判断B 是否存在 tail([X,Y])=[Y] 中，不存在，提出B，得到：

L(F) = F + merge([A,X,Y],[B,X,Y]) = [F,A] + merge([X,Y],[B,X,Y]) = [F,A,B] + merge([X,Y],[X,Y])

剩下逻辑一样，依次提出 X和Y:

L(F) = F + merge([A,X,Y],[B,X,Y]) = [F,A] + merge([X,Y],[B,X,Y]) = [F,A,B] + merge([X,Y],[X,Y]) = [F,A,B,X,Y]

可以将我上述python代码运行一下结果和我们手算的是一样的：

(<class '__main__.F'>, <class '__main__.A'>, <class '__main__.B'>, <class '__main__.X'>, <class '__main__.Y'>, <class 'object'>)

复杂的解析(练手逻辑)

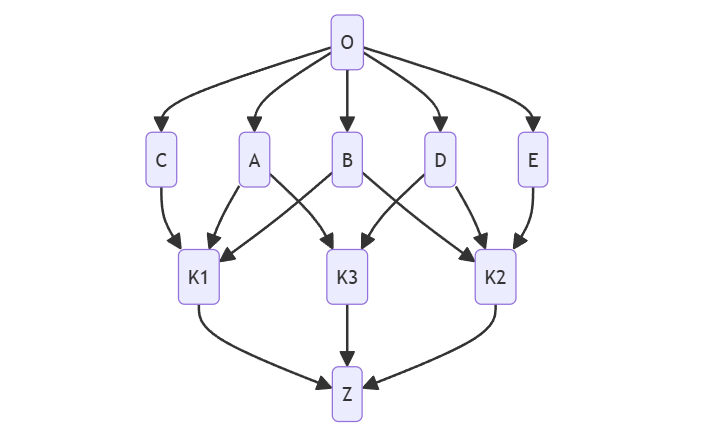
L(K1) = K1 + merge(L(C), L(A), L(B))
      = K1 + merge([C, O], [A, O], [B, O])
      = [K1, C] + merge([O], [A, O], [B, O])
      = [K1, C, A] + merge([O], [O], [B, O])
      = [K1, C, A, B] + merge([O], [O], [O])
      = [K1, C, A, B, O]
L(K2) = [K2, B,D,E, O]
L(K3) = [K3,A, D, O]
L(Z)  = Z + merge(L(K1), L(K3), L(K2))
      = Z + merge([K1, C, A, B, O],[K3, A, D, O],[K2, B, D, E, O])
      = [Z, K1] + merge([C, A, B, O], [K3, A, D, O], [K2, B, D, E, O])
      = [Z, K1, C] + merge([A, B, O], [K3, A, D, O], [K2, B, D, E, O])
      = [Z K1, C] + merge([A, B, O],  [K3, A, D, O], [K2, B, D,E, O])
      = [Z, K1, C, K3] + merge([A, B, O], [A, D, O], [K2, B, D, E, O])
      = [Z, K1, C, K3, A] + merge([B, O], [D, O],  [K2, B, D, E, O])
      = [Z,K1, C, K3, A, K2] + merge([B, O], [D, O], [B, D, E, O])
      = [Z,K1, C, K3, A, K2, B] + merge([O], [D, O], [D, E, O])
      = [Z, K1,C, K3, A, K2, B, D] + merge([O], [O], [E,O])
      = [Z, K1,C, K3, A, K2, B, D, E, O]

class O:
    pass

class C(O):
    pass

class A(O):
    pass

class B(O):
    pass

class D(O):
    pass

class E(O):
    pass

class K1(C,A,B):
    pass

class K3(A,D):
    pass

class K2(B,D,E):
    pass

class Z(K1,K3,K2):
    pass

print(Z.__mro__)

手写C3算法

def c3MRO(cls):
    if cls is object:
        # 讨论假设顶层基类为object，递归终止
        return [object]

    # 构造C3-MRO算法的总式，递归开始
    mergeList = [c3MRO(baseCls) for baseCls in cls.__bases__]
    mergeList.append(list(cls.__bases__))
    mro = [cls] + merge(mergeList)
    return mro

def merge(inLists):
    if not inLists:
        # 若合并的内容为空，返回空list
        # 配合下文的排除空list操作，递归终止
        return []

    # 遍历要合并的mro
    for mroList in inLists:
        # 取head
        head = mroList[0]
        # 遍历要合并的mro（与外一层相同），检查尾中是否有head
        ### 此处也遍历了被取head的mro，严格地来说不符合标准算法实现
        ### 但按照多继承中地基础规则（一个类只能被继承一次），
        ### head不可能在自己地尾中，无影响，若标准实现，反而增加开销
        for cmpList in inLists[inLists.index(mroList) + 1:]:
            if head in cmpList[1:]:
                break
        else:
            # 筛选出好head
            nextList = []
            for mergeItem in inLists:
                if head in mergeItem:
                    mergeItem.remove(head)
                if mergeItem:
                    # 排除空list
                    nextList.append(mergeItem)
            # 递归开始
            return [head] + merge(nextList)
    else:
        # 无好head，引发类型错误
        raise TypeError

参考文章：

c3 linearization详解 - Hello_wshuo - 博客园

Python多重继承问题之MRO和C3算法_Python_王坤祥_InfoQ写作社区