leetcode每日一题：酿造药水需要的最少总时间

引言

​ 今天的每日一题原题是2255. 统计是给定字符串前缀的字符串数目，直接模拟，逐个匹配words中的字符串是否是s的前缀即可。更换成前几天遇到的更有意思的一题来写这个每日一题。

题目

给你两个长度分别为 n 和 m 的整数数组 skill 和 mana 。

在一个实验室里，有 n 个巫师，他们必须按顺序酿造 m 个药水。每个药水的法力值为 mana[j]，并且每个药水 必须 依次通过 所有 巫师处理，才能完成酿造。第 i 个巫师在第 j 个药水上处理需要的时间为 timeij = skill[i] * mana[j]。

由于酿造过程非常精细，药水在当前巫师完成工作后 必须 立即传递给下一个巫师并开始处理。这意味着时间必须保持 同步，确保每个巫师在药水到达时 马上 开始工作。

返回酿造所有药水所需的 最短 总时间。

示例 1：

输入： skill = [1,5,2,4], mana = [5,1,4,2]

输出： 110

解释：

药水编号	开始时间	巫师 0 完成时间	巫师 1 完成时间	巫师 2 完成时间	巫师 3 完成时间
0	0	5	30	40	60
1	52	53	58	60	64
2	54	58	78	86	102
3	86	88	98	102	110

举个例子，为什么巫师 0 不能在时间 t = 52 前开始处理第 1 个药水，假设巫师们在时间 t = 50 开始准备第 1 个药水。时间 t = 58 时，巫师 2 已经完成了第 1 个药水的处理，但巫师 3 直到时间 t = 60 仍在处理第 0 个药水，无法马上开始处理第 1个药水。

示例 2：

输入： skill = [1,1,1], mana = [1,1,1]

输出： 5

解释：

1. 第 0 个药水的准备从时间 t = 0 开始，并在时间 t = 3 完成。
2. 第 1 个药水的准备从时间 t = 1 开始，并在时间 t = 4 完成。
3. 第 2 个药水的准备从时间 t = 2 开始，并在时间 t = 5 完成。

示例 3：

输入： skill = [1,2,3,4], mana = [1,2]

输出： 21

提示：

• n == skill.length
• m == mana.length
• 1 <= n, m <= 5000
• 1 <= mana[i], skill[i] <= 5000

思路

​ 首先要读懂题目，有个关键点是，对于同一瓶药水，在前一个巫师处理完成后，立即传递给下一个巫师进行处理。所以，这里跟直觉的贪心有一些区别，对于同一个巫师，处理一瓶药水后，并不能马上去处理下一瓶药水，要确保自己处理完成后，后一个巫师是空闲的状态。

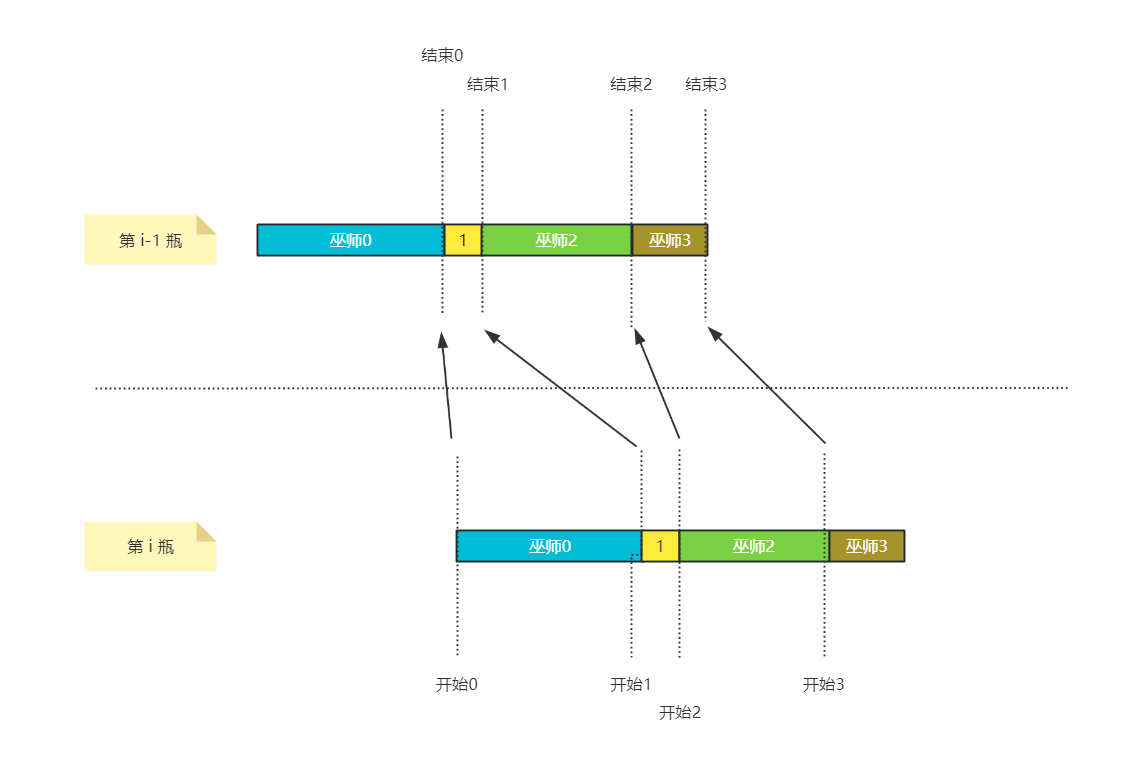
​ 读懂了这个点，我们来看第i瓶药水的处理，假设我们记第i瓶药水是从第beginDelay的时刻开始处理，而每个巫师处理上一瓶（第i-1瓶）药水的完成时间为end[]，我们来看看这个beginDelay需要满足哪些条件：

• 对于第0个巫师，自己的开始处理时间是beginDelay，必须晚于等于上一瓶结束时间，保证开始处理第i瓶是，自己是空闲的，即满足 beginDelay >= end[0]；
• 对于第1个巫师，自己的开始处理时间是beginDelay + skill[i] * mana[0]，必须晚于等于上一瓶结束时间，即满足 beginDelay + skill[i] * mana[0] >= end[1]；
• 对于第2个巫师，自己的开始处理时间是beginDelay + skill[i] * (mana[0] + mana[1])，必须晚于等于上一瓶结束时间，即满足 beginDelay + skill[i] * (mana[0] + mana[1]) >= end[1]；
• 后面的巫师可以以此类推

​ 这样，如果我们有n个巫师，对于第i瓶药水，就会有n个不等式，贪心的，求出满足这n个不等式的最小beginDelay，就可以求出对于第i瓶药水每个巫师的最早完成时间，用于列出第i+1瓶要求的不等式。特别的，对于第0瓶药水，当前每个巫师都是空闲的，可以认为end[]数组的值都是0。

​ 另外，不等式中，我们对每瓶要求都会去求出mana[0]、mana[0] + mana[1]、mana[0] + mana[1] + mana[2] 这样的值，可以事先求一次前缀和，避免重复计算。

图解

代码

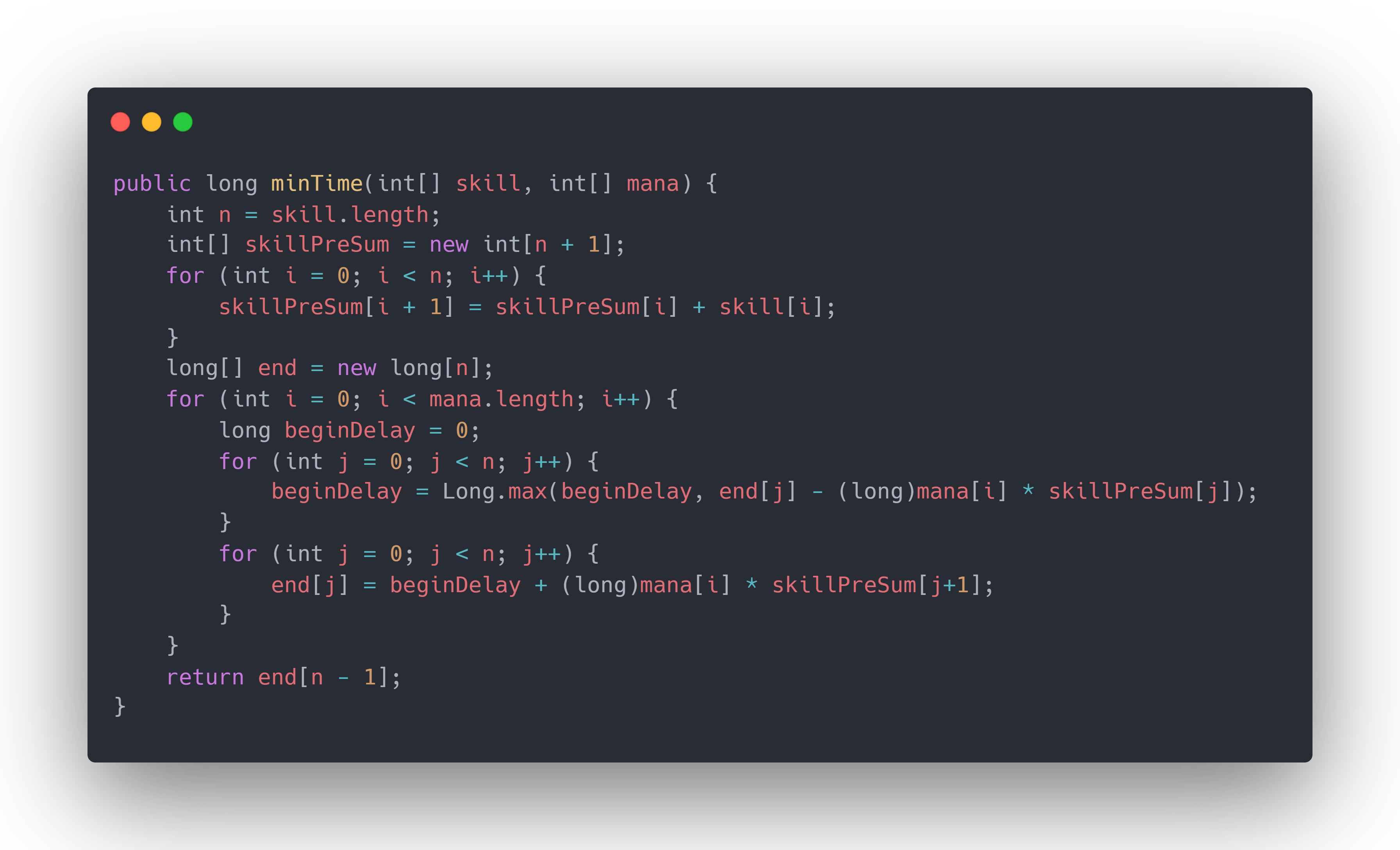
public long minTime(int[] skill, int[] mana) {
    int n = skill.length;
    int[] skillPreSum = new int[n + 1];
    for (int i = 0; i < n; i++) {
        skillPreSum[i + 1] = skillPreSum[i] + skill[i];
    }
    long[] end = new long[n];
    for (int i = 0; i < mana.length; i++) {
        long beginDelay = 0;
        for (int j = 0; j < n; j++) {
            beginDelay = Long.max(beginDelay, end[j] - (long)mana[i] * skillPreSum[j]);
        }
        for (int j = 0; j < n; j++) {
            end[j] = beginDelay + (long)mana[i] * skillPreSum[j+1];
        }
    }
    return end[n - 1];
}

耗时