字符串算法--$\mathcal{KMP，Trie}$树

\(\mathcal{KMP算法}\)

实际上，完全没必要从\(S\)的每一个字符开始，暴力穷举每一种情况，\(Knuth、Morris\)和\(Pratt\)对该算法进行了改进，称为KMP算法。

而\(KMP\)的精髓在于，对于每次失配之后，我都不会从头重新开始枚举，而是根据我已经得知的数据，从某个特定的位置开始匹配；而对于模式串的每一位，都有唯一的“特定变化位置”，这个在失配之后的特定变化位置可以帮助我们利用已有的数据不用从头匹配，从而节约时间。

特点：1. \(i\) 不回退 2. \(j\) 回退的位置有讲究 3.构建一个辅助数组（ \(nxt\) 数组）来跳过不必要的字符比较，从而提高搜索速度。

\(\mathcal{实现流程}\)

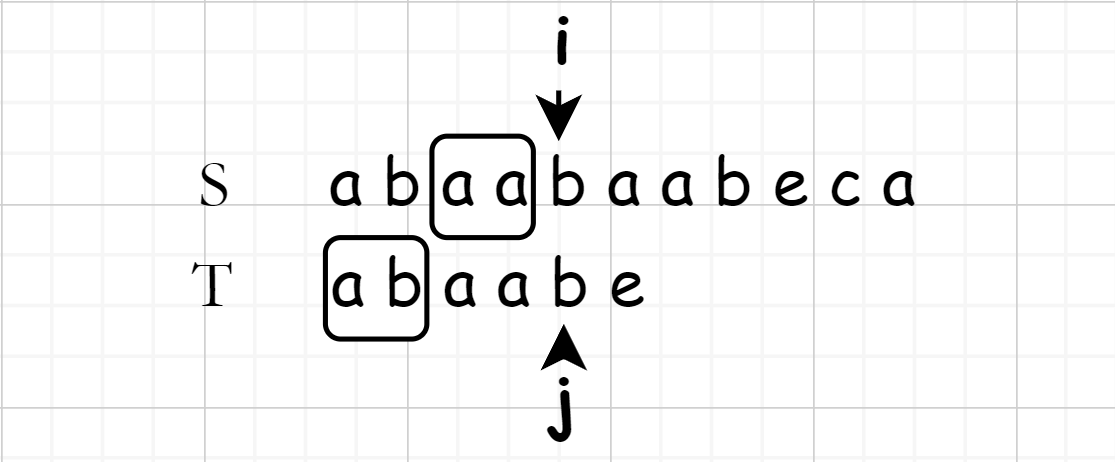
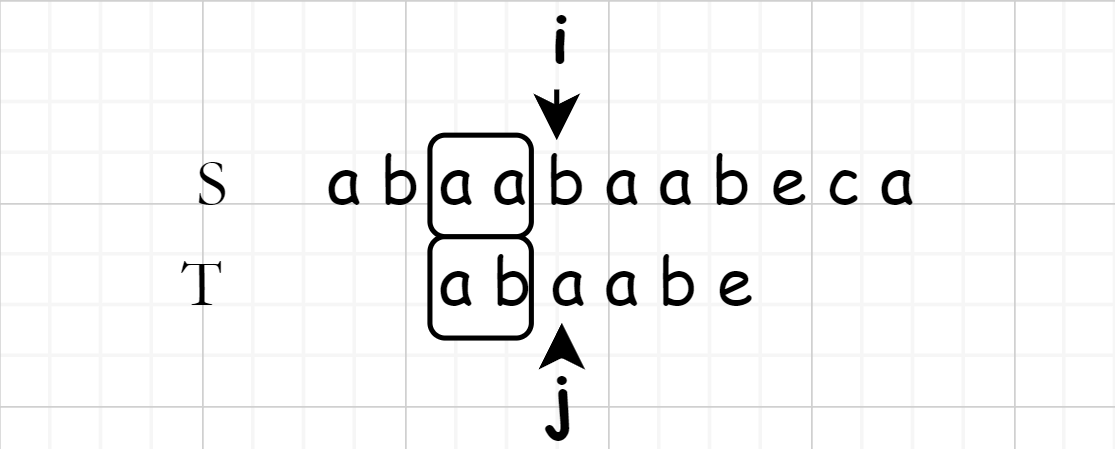
为了清楚地表述目的， \(T\) 与 \(S\) 失配前的部分作为 \(T'\) 来表述，此时寻找下一个开始匹配的标志头。而找到下一个标志头的方式为：

找到 \(T'\) 的最长相同前缀与后缀

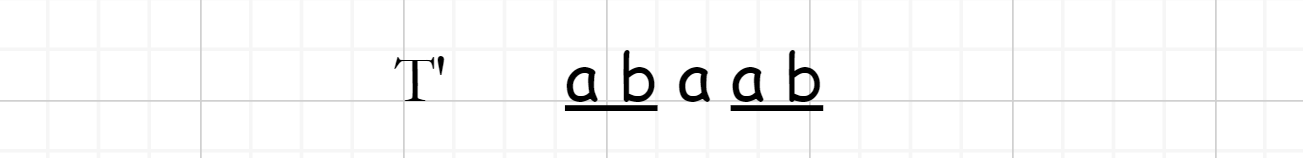
\(\color{red}{这样找所有的前缀和后缀比较，是不是也是暴力穷举？？那该怎么办呢？？}\)

\(\color{red}{ans:当然是要用到动态规划递推啦。}\)

\(\mathcal{构建 Nxt 数组}\)

\(nxt\) 数组用于表示当前字符匹配失败时，模式串应该回退到哪个位置。对于模式串 \(p\) ，我们遍历其每个字符，并用一个指针 \(j\) 表示已匹配的字符数。当模式串中的两个字符匹配时，我们更新指针 \(j\) 的值，否则，我们回退 \(j\) 到 \(nxt[j]\) 的位置。通过这种方式，我们可以为模式串构建一个 \(nxt\) 数组，其中 \(nxt[i]\) 表示当模式串中第 \(i\) 个字符匹配失败时，应该回退到的位置。

\(\mathcal{实际字符匹配过程}\)

我们使用两个指针 \(i\) 和 \(j\) 分别遍历原字符串 \(s\) 和模式串 \(p\) 。如果当前字符匹配，则同时移动 \(i\) 和 \(j\) 。如果字符不匹配，我们根据 \(nxt\) 数组回退 \(j\) 的位置，直到找到匹配的字符或回退到模式串的开头。当 \(j\) 等于模式串长度 \(m\) 时，表示找到了一个匹配，输出匹配位置，并将 \(j\) 重置为 \(0\) 。

\(\mathcal{模板代码实现}\)

#include <iostream>
using namespace std;
const int N = 1e+6 + 10;
int nxt[N], n, m;
char p[N], s[N];
int main()
{
    cin >> n >> s + 1 >> m >> p + 1;
    // build next arraylist
    for (int i = 2, j = 0; i <= m; i++)
    {
        while (j && p[i] != p[j + 1]) j = nxt[j];
        if (p[i] == p[j + 1]) j++;
        nxt[i] = j;
    }
    // marry the str
    for (int i  = 1, j = 0; i <= n; i++)
    {
        while (j && s[i] != p[j + 1]) j = nxt[j];
        if (s[i] == p[j + 1]) j++;
        if (j == m) {
            cout << i - m << " ";
            j = 0;
        }
    }
    cout << endl;
    return 0;
}

\(\mathcal{Trie\,树}\)

字典树是一种高效的字符串数据结构，尤其适用于处理大量字符串的时候，它通过将字符串的公共前缀合并在一起，节省空间并提高查询速度。

\(\mathcal{实现流程}\)

\(\mathcal{初始化变量和数据结构}\)

定义一个字典树结构（ \(tree\) 数组）和一个记录字符串出现次数的数组（ \(vis\) 数组）。同时定义一个计数器 \(flag\) 用于记录字典树中节点的数量。二维数组 \(tree\) 表示字典树的结构，其中 \(tree[i][j]\) 表示第 \(i\) 个节点的第 \(j\) 个子节点。

\(\mathcal{子功能实现}\)

\(\mathcal{insert}\)

实现一个 \(insert\) 函数，用于向字典树中插入一个字符串。它遍历字符串中的每个字符，将字符转换为数组下标（通过减去' \(a\) '并加上 \(1\) ）。如果当前字符对应的子节点不存在，则创建一个新的节点并更新节点计数器。最后，在字符串末尾的节点中，更新字符串出现的次数。

\(\mathcal{query}\)

实现一个 \(query\) 函数，用于查询字典树中字符串的出现次数。它遍历字符串中的每个字符，将字符转换为数组下标。如果当前字符对应的子节点不存在，说明字符串不存在，查询结束。否则，将指针移动到子节点。最后，返回字符串末尾节点对应的出现次数。

\(\mathcal{主程序逻辑}\)

读取操作数量 \(n\) ，然后循环处理每个操作。对于每个操作，读取操作类型（ \(ope\) ）和操作字符串（ \(str\) ）。如果操作类型为 "\(i\)" ，调用 \(insert\) 函数插入字符串；如果操作类型为其他（例如查询操作），调用 \(query\) 函数查询字符串，并输出查询结果。

\(\mathcal{模板代码实现}\)

#include <iostream>
using namespace std;
const int N = 1e+6 + 10;
int n, flag = 1;
string ope, str;
int tree[N][27], vis[N][27];
void insert(string str)
{
    int pos = 0;
    int tmp = 0;
    for (int i = 0; i < str.size(); i++)
    {
        tmp = str[i] - 'a' + 1;
        if (tree[pos][tmp] == 0) tree[pos][tmp] = flag ++;
        pos = tree[pos][tmp];
    }
    vis[pos][tmp] ++;
}
int query(string str)
{
    int pos = 0;
    int tmp = 0;
    for (int i  = 0; i < str.size(); i++)
    {
        tmp = str[i] - 'a' + 1;
        if (tree[pos][tmp] == 0) break;
        pos = tree[pos][tmp];
    }
    return vis[pos][tmp];
}
int main()
{
    cin >> n;
    while (n--)
    {
        cin >> ope >> str;
        if (ope == "i") insert(str);
        else cout << query(str) << endl;
    }
    return 0;
}