双调排序--GPU/AIPU适合的排序【转载】

欢迎转载，转载请注明：本文出自Bin的专栏blog.csdn.net/xbinworld
技术交流QQ群：433250724，欢迎对算法、技术、应用感兴趣的同学加入

双调排序是data-independent的排序，即比较顺序与数据无关的排序方法，特别适合做并行计算，例如用GPU、fpga来计算。

1、双调序列

在了解双调排序算法之前，我们先来看看什么是双调序列。双调序列是一个先单调递增后单调递减（或者先单调递减后单调递增）的序列。

2、Batcher定理

将任意一个长为2n的双调序列A分为等长的两半X和Y，将X中的元素与Y中的元素一一按原序比较，即a[i]与a[i+n] (i <
n)比较，将较大者放入MAX序列，较小者放入MIN序列。则得到的MAX和MIN序列仍然是双调序列，并且MAX序列中的任意一个元素不小于MIN序列中的任意一个元素[2]。

3、双调排序

假设我们有一个双调序列，则我们根据Batcher定理，将该序列划分成2个双调序列，然后继续对每个双调序列递归划分，得到更短的双调序列，直到得到的子序列长度为1为止。这时的输出序列按单调递增顺序排列。

见下图：升序排序，具体方法是，把一个序列(1…n)对半分，假设n=2^k，然后1和n/2+1比较，小的放上，接下来2和n/2+2比较，小的放上，以此类推；然后看成两个(n/2)长度的序列，因为他们都是双调序列，所以可以重复上面的过程；总共重复k轮，即最后一轮已经是长度是2的序列比较了，就可得到最终的排序结果。

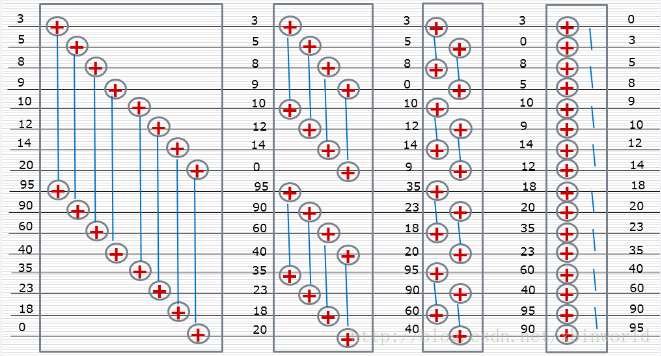
双调排序示意图[1]:

4、任意序列生成双调序列

前面讲了一个双调序列如何排序，那么任意序列如何变成一个双调序列呢？

这个过程叫Bitonic merge, 实际上也是divide and conquer的思路。和前面sort的思路正相反，
是一个bottom up的过程——将两个相邻的，单调性相反的单调序列看作一个双调序列，
每次将这两个相邻的，单调性相反的单调序列merge生成一个新的双调序列，然后排序（同3、双调排序）。
这样只要每次两个相邻长度为n的序列的单调性相反，
就可以通过连接得到一个长度为2n的双调序列，然后对这个2n的序列进行一次双调排序变成有序，然后在把两个相邻的2n序列合并（在排序的时候第一个升序，第二个降序）。
n开始为1，每次翻倍，直到等于数组长度，最后就只需要再一遍单方向（单调性）排序了。

以16个元素的array为例，
1. 相邻两个元素合并形成8个单调性相反的单调序列，
2. 两两序列合并，形成4个双调序列，分别按相反单调性排序
3. 4个长度为4的相反单调性单调序列，相邻两个合并，生成两个长度为8的双调序列，分别排序
4. 2个长度为8的相反单调性单调序列，相邻两个合并，生成1个长度为16的双调序列，排序

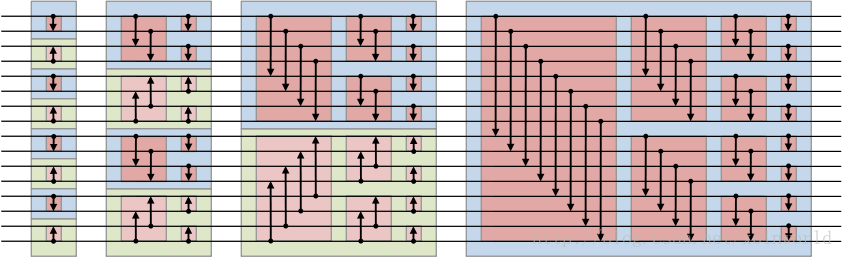
示意图[1]：

详细Bitonic merge图（本图只画到生成一个16长的双调序列，最后排序没有画出）：

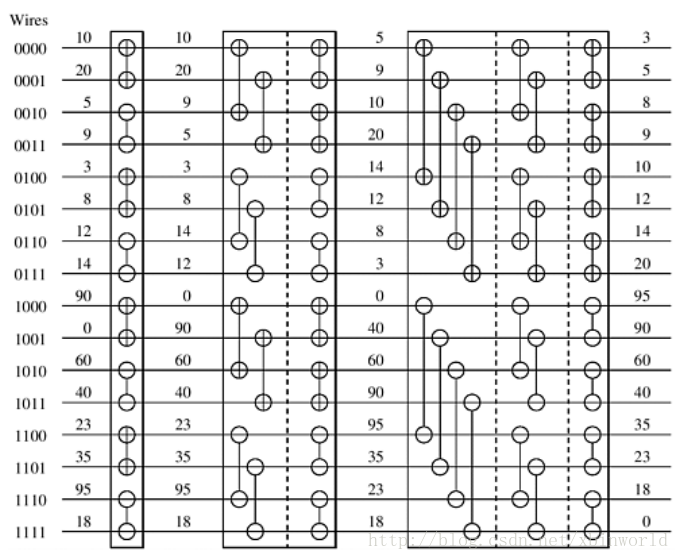
最后再放一个8个元素排序的示意图[5]：

5、非2的幂次长度序列排序

这样的双调排序算法只能应付长度为2的幂的数组。那如何转化为能针对任意长度的数组呢？一个直观的方法就是使用padding。即使用一个定义的最大或者最小者来填充数组，让数组的大小填充到2的幂长度，再进行排序。最后过滤掉那些最大（最小）值即可。这种方式会使用到额外的空间，而且有时候padding的空间比较大（如数组长度为1025个元素，则需要填充到2048个，浪费了大量空间）。但是这种方法比较容易转化为针对GPU的并行算法。所以一般来说，并行计算中常使用双调排序来对一些较小的数组进行排序[3]。
如果要考虑不用padding，用更复杂的处理方法，参考[4] n!=2^k的双调排序网络，本文略。

参考资料

[1] CUDA(六). 从并行排序方法理解并行化思维——冒泡、归并、双调排序的GPU实现, http://blog.csdn.net/abcjennifer/article/details/47110991
[2] 并行计算】Bitonic Sort（双调排序）基础, http://blog.csdn.net/jiange_zh/article/details/49533477
[3] 双调排序：从串行到并行，以及OpenCL上的实现, http://blog.csdn.net/bryanlai0720/article/details/45094675
[4] n!=2^k的双调排序网络, http://blog.csdn.net/ljiabin/article/details/8630627
[5] 分段双调排序实现, http://blog.csdn.net/u014226072/article/details/56840243