运筹学笔记12 大M法

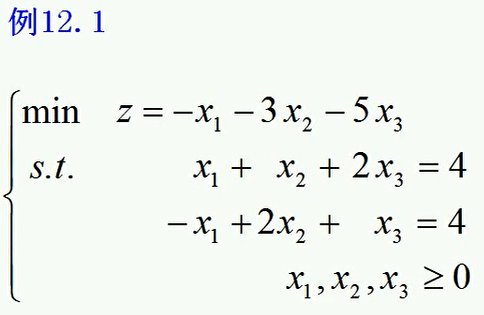
引入M，其中M是一个充分大的正数。由此，目标函数也改变为zM.

如此构造的线性规划问题我们记作LPM，称之为辅助线性规划问题，也即在原来的线性规划问题的基础上，改造了其等式约束条件，然后有对目标函数施加了惩罚项，Mx4,Mx5。

因为M是充分大的正数，所以即便x4,x5很小，只要x4,x5不等于0，这个惩罚项也也会很大的；一旦大M趋于正无穷，那么Mx4,Mx5一块就是正无穷了；而前面的各变量及其系数

的组合也是有限的量；根据一个有限的量加上一个无穷大量结果是无穷大量定理；那么目标函数就是趋于无穷大量，怎么还会取得最小值呢？∴大M叫做惩罚项是有道理的，而且

在理想的状态下，一旦x4,x5取值为零，那么目标函数中就再也没有惩罚项了，目标函数也就有zM还原为z了，同时约束条件x4,x5也就消失了，因为二者此时为零；

这样也就实现了有LPM向原线性规划问题的还原。所以大M法，首先引入大M惩罚项，对人为引入的人工变量施加惩罚，最佳的状态就是把引入的人工变量都惩罚为0，这样不仅等式约束条件没被破坏，目标函数也还原为原来的目标函数了。如果做不到这一步，就说明有些约束条件原来就不可能相等。

我们构造辅助线性规划问题后可看到已经有x4,x5系数组成的单位矩阵了，我们把它取作初始可行基。

进而可以写出典式的等价形式(把基变量和目标函数都用非基变量表示)如下：

进而做出单纯形表：

有了单纯形表，进一步讨论三种情形。

情形1：是否全部的检验数都<=0;很显然此题不是；1肯定是>0的，另外M是充分大的正数所以3M+3,3M+5也都是>=0的。

情形2：正的检验数上面没有正的，才是第二种情况；此题不符合；

显然是第三种情况了，选定枢轴列->元，然后转轴。

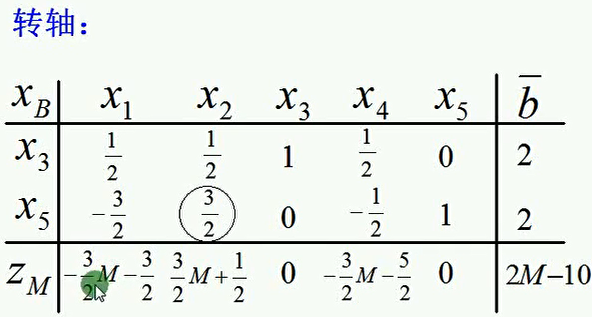
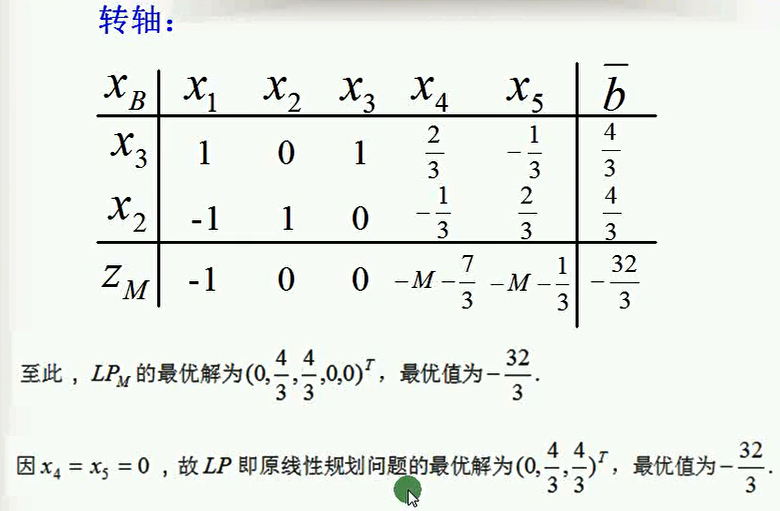
上图得到了辅助线性规划问题的最优解和最优值，但须注意，在辅助线性规划问题中，我们引入了两个人工变量的值，x4,x5,

也可发现在LPM的最优解中两个变量都已经为0了。也即是说，辅助线性规划的人工变量都已经被充分大的大M构造的惩罚项惩罚为0了，也就是说又还原为原来初始的线性规划问题了，所以据此我们就可以得到LP，即原来线性规划问题的最优解和最优值。。。

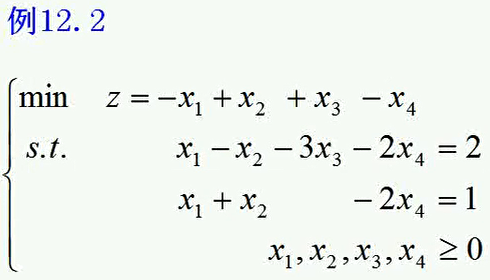
可看到上图中有一个检验数是正的，其所在列上面的值都是<=0，所以是第二种情形，所以LPM无下届。

而之前引入的人工变量x5对应的取值为1，并没有被惩罚为0；另一个非基变量x6作为非基变量已经被惩罚为0了；

也即，因x5=1,x6=0,故原线性规划问题不可行。

练习：