JZOJ 4296. 有趣的有趣的家庭菜园

【NOIP2015模拟11.2】有趣的有趣的家庭菜园

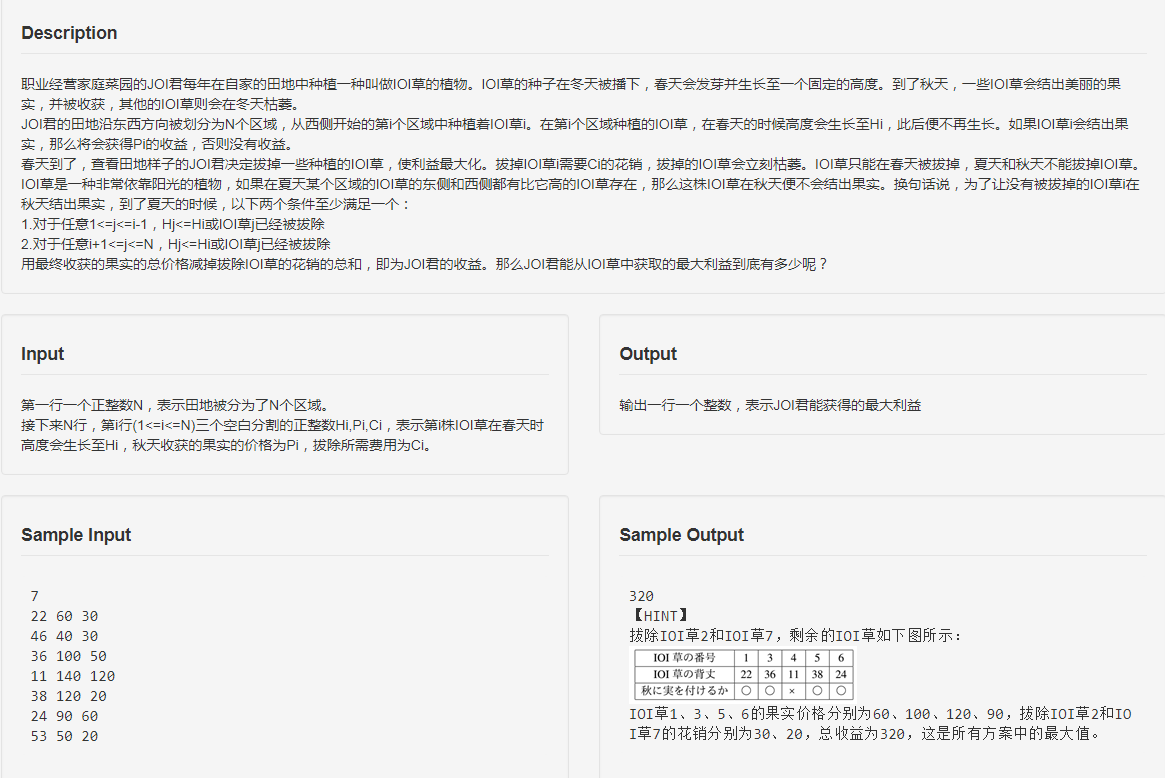
题面

思路一

暴力 \(30\) 分！

很容易打，但是要注意：

• 开 \(\texttt{long long}\)
• 是非严格高于（等于是被允许的）

思路二

发现 \(i\) 能收获的条件是只要他为其中一侧的最大值

那么我们设 \(f_i\) 表示 \(1..i\) 中必选 \(i\) 的答案，\(g_i\) 表示 \(i..n\) 中必选 \(i\) 的答案

那么答案就是 \(\max_{i=1}^n{f[i]+g[i]-val[i]}\)，其中 \(val[i]\) 表示 \(i\) 草收获果实的贡献。

因为根据 \(f,g\) 的定义可得 \(i\) 处两者都算了，所以就减去重复的贡献

那么考虑怎么求 \(f,g\)

既然两者一个是顺着，一个是倒着，那么我们不妨讨论 \(f\)，\(g\) 同理

思考 \(i\) 从 \(j\) 处转移过来，\((i,j)\) 间比 \(i\) 高的草都要除掉

那么 \(f_i = \max(f_j - \sum_{k=j+1}^{i-1} cost_k·[h_k > h_i])(0 \leq j < i)\)

\(cost_k\) 为除掉 \(k\) 所需的费用

它显然是 \(O(n^3)\) 的

我们要考虑优化

思考我们是如何进行转移的？

感性的理解，我们找到 \(j\)，把 \(j\) 到 \(i\) 间比 \(i\) 高的草都删除再转移到 \(i\)

那么我们能不能考虑一次性找到最大的 \(f_j - \sum_{k=j+1}^{i-1} cost_k·[h_k > h_i]\)

发现限制条件是 \(h_k > h_i\)

也就是说从左一次往右时 \(h_i\) 会影响比他矮的节点，\(f_j - \sum_{k=j+1}^{i-1} cost_k·[h_k > h_i]\) 就是开区间 \((i..j)\) 中比 \(j\) 高的所有草费用之和

即遇到一个 \(h_i\) 时就算它的影响

于是我们可以用线段树维护，对草的高度先离散化，再对高度建一颗线段树

对于当前点 \(i\)，先找线段树 \([1..h_i]\) 中权值最大的点更新 \(f_i\)

然后让线段树中 \([1..h_i-1]\) 的值减去 \(cost_i\)

最后把 \(f_i\) 插入线段树中 \(h_i\) 的位置

终了统计一下答案

正好温习一下线段树的区间加，区间最值，单点修改

记得打懒标记哦！！

\(Code\)

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;

const int N = 1e5 + 5;
int n;
LL seg[N << 2] , tag[N << 2] , f[N] , g[N] , ans;

struct node{
	int hign , h , p , c , id;
}a[N];

inline bool cmp(node x , node y){return x.hign < y.hign;}
inline bool cmp1(node x , node y){return x.id < y.id;}

inline void pushup(int k){seg[k] = max(seg[k << 1] , seg[k << 1 | 1]);}
inline void pushdown(int k)
{
	if (tag[k] != 0)
	{
		seg[k << 1] += tag[k];
		tag[k << 1] += tag[k];
		seg[k << 1 | 1] += tag[k];
		tag[k << 1 | 1] += tag[k];
		tag[k] = 0;
	}
}

inline void update(int x , LL y , int l , int r , int k)
{
	if (l == r && l == x)
	{
		seg[k] = max(seg[k] , y);
		return;
	}
	pushdown(k);
	int mid = (l + r) >> 1;
	if (x <= mid) update(x , y , l , mid , k << 1);
	else update(x , y , mid + 1 , r , k << 1 | 1);
	pushup(k);
}

inline void change(int x , int y , LL v , int l , int r , int k)
{
	if (x <= l && r <= y)
	{
		tag[k] += v;
		seg[k] += v;
		return;
	}
	pushdown(k);
	int mid = (l + r) >> 1;
	if (x <= mid) change(x , y , v , l , mid , k << 1);
	if (y > mid) change(x , y , v , mid + 1 , r , k << 1 | 1);
	pushup(k);
}

inline LL query(int x , int y , int l , int r , int k)
{
	if (x <= l && r <= y) return seg[k];
	pushdown(k);
	LL res = -1e18;
	int mid = (l + r) >> 1;
	if (x <= mid) res = max(res , query(x , y , l , mid , k << 1));
	if (y > mid) res = max(res , query(x , y , mid + 1 , r , k << 1 | 1));
	return res;
}	

int main()
{
	freopen("herbary.in" , "r" , stdin);
	freopen("herbary.out" , "w" , stdout);
	scanf("%d" , &n);
	for(register int i = 1; i <= n; i++) scanf("%d%d%d" , &a[i].hign , &a[i].p , &a[i].c) , a[i].id = i;
	sort(a + 1 , a + n + 1 , cmp);
	a[1].h = 1;
	int s = 1;
	for(register int i = 2; i <= n; i++)
	{
		if (a[i].hign == a[i-1].hign) a[i].h = a[i-1].h;
		else a[i].h = ++s;
	}
	sort(a + 1 , a + n + 1 , cmp1);

	memset(seg , 0 , sizeof seg);
	memset(tag , 0 , sizeof tag);
	for(register int i = 1; i <= n; i++)
	{
		f[i] = query(1 , a[i].h , 1 , s , 1) + a[i].p;
		update(a[i].h , f[i] , 1 , s , 1);
		if (a[i].h > 1) change(1 , a[i].h - 1 , -a[i].c , 1 , s , 1);
	}

	memset(seg , 0 , sizeof seg);
	memset(tag , 0 , sizeof tag);
	for(register int i = n; i; i--)
	{
		g[i] = query(1 , a[i].h , 1 , s , 1) + a[i].p;
		update(a[i].h , g[i] , 1 , s , 1);
	    if (a[i].h > 1) change(1 , a[i].h - 1 , -a[i].c , 1 , s , 1);
	}

	for(register int i = 1; i <= n; i++) ans = max(ans , f[i] + g[i] - a[i].p);
	printf("%lld" , ans);
}