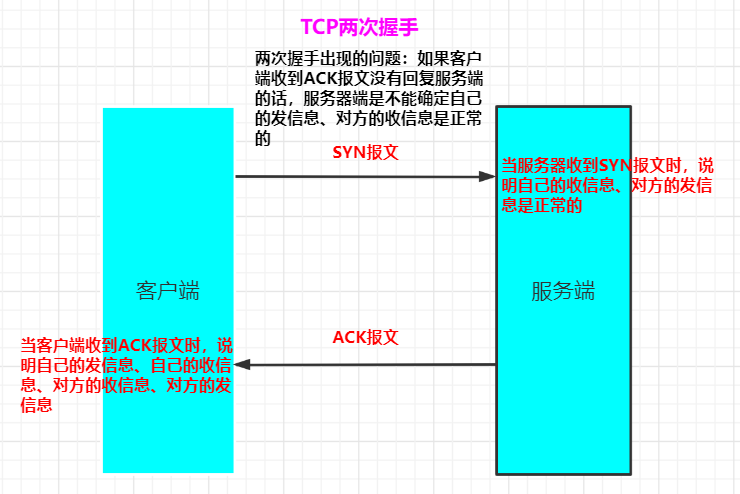
两次握手

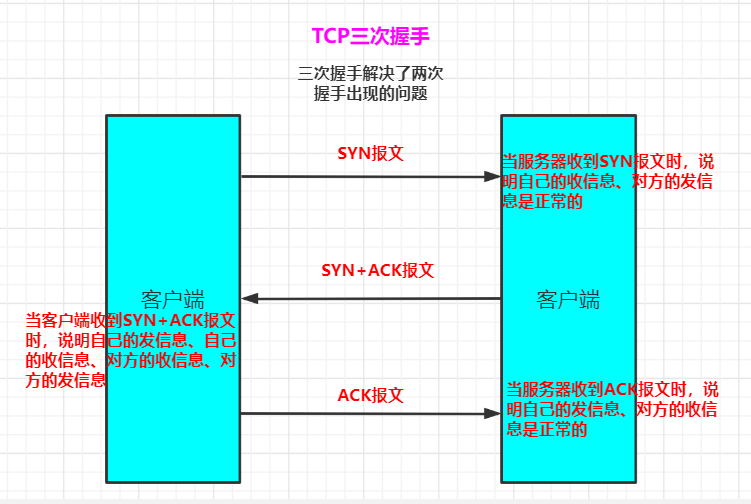
 三次握手

为什么 TCP 链接需要三次握手，两次不可以么，为什么？的更多相关文章

  1. TCP链接的三次握手与四次断开

    一直总觉得三次握手和四次断开,之前老师讲的有问题,经过自己再次琢磨,发现是的,老师讲的没毛病,这次也把自己的理解总结一下,让对这个知识模糊的小伙伴再换种思路去理解 首先看一下TCP三次握手发生了哪些: ...

  2. TCP 为什么是三次握手，而不是两次或四次？

    TCP是一种全双工的可靠传输协议,核心思想:保证数据可靠传输以及数据的传输效率 A------B 二次握手: 1.A发送同步信号SYN+A's initial sequence number 2.B发 ...

  3. TCP连接建立的三次握手过程可以携带数据吗？

    前几天实验室的群里扔出了这样一个问题:TCP连接建立的三次握手过程可以携带数据吗?突然发现自己还真不清楚这个问题,平日里用tcpdump或者Wireshark抓包时,从来没留意过第三次握手的ACK包有 ...

  4. TCP/IP协议三次握手和四次挥手大白话解说

    前言 昨天晚上被一位师傅问到了TCP/IP的工作机制,心里很清楚三次握手,然而对于四次挥手却忘了,这是大学习里学过的,奋而翻阅书籍和网络对之前所学的做一个温顾,算是夯实自我吧. TCP(Transmi ...

  5. python网络编程--TCP连接的三次握手(三报文握手)与四次挥手

    一.TCP连接 运输连接有三个阶段: 连接建立.数据传送和连接释放. 在TCP连接建立过程中要解决以下三个问题: 1,要使每一方能够确知对方的存在. 2.要允许双方协商一些参数(如最大窗口之,是否使用 ...

  6. TCP 中的三次握手和四次挥手

    Table of Contents 前言 数据报头部 三次握手 SYN 攻击 四次挥手 半连接 TIME_WAIT 结语 参考链接 前言 TCP 中的三次握手和四次挥手应该是非常著名的两个问题了,一方 ...

  7. 详解TCP连接的“三次握手”与“四次挥手”(下)

    上文链接: 详解TCP连接的"三次握手"与"四次挥手"(上) 四.TCP的四次挥手(Four-Way Wavehand) 0.前言 对于"三次握手&q ...

  8. CCNA-Part5 - 传输层 ，TCP 为什么是三次握手？

    传输层 传输层主要的作用就是建立端到端的连接.比如电脑的微信的通信,就需要跨越多个网络设备(交换机和录取)再和微信的服务器建立连接. 传输层需要具有以下的特点: 会话的多复用:如电脑上开启的多个应用, ...

  9. TCP/IP协议三次握手与四次握手流程解析

    原文链接地址:http://www.2cto.com/net/201310/251896.html TCP/IP协议三次握手与四次握手流程解析 TCP/IP协议的详细信息参看<TCP/IP协议详 ...

随机推荐

  1. onerror事件捕获网页中的错误

    转载请注明来源:https://www.cnblogs.com/hookjc/ <html><head><script type="text/javascrip ...

  2. nginx开发：ngx_sprintf

    格式化参数%系列,如果误用的话,轻则输出不正确,重则nginx可能core. 1. 格式: %{格式描述}{输出类型描述}{数据类型描述} 2. 数据类型描述: V:字符串,对应ngx_str_t * ...

  3. bom-scroll

    <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...

  4. JspSmartUpload 简略使用

    JspSmartUpload 简略中文API文档 链接:https://blog.csdn.net/weixin_43670802/article/details/105143830 PDF课件 链接 ...

  5. iOS App 架构文章推荐

    iOS应用开发架构 iOS应用架构谈系列 阿里技术沙龙 2.2.1. Hybrid App 2.2.2. taobao 客户端架构 2.2.3. alipay 客户端架构   iOS APP 架构漫谈 ...

  6. 关于CSP-S2019的一篇游记

    怎么讲呢? Day1:7:00左右从家里出发,准备还是做得比较充分,早饭也记得吃了.路上闭目养神了一会儿,7:50左右到了大门附近,和大家再次把一些自认为还是比较重要的数据结构之类的再复习了一下.进去 ...

  7. Java泛型详解，史上最全图文详解！

    泛型在java中有很重要的地位,无论是开源框架还是JDK源码都能看到它. 毫不夸张的说,泛型是通用设计上必不可少的元素,所以真正理解与正确使用泛型,是一门必修课. 一:泛型本质 Java 泛型(gen ...

  8. Vue.use初探

    Vue.use 问题 相信很多人在用Vue使用别人的组件时,会用到 Vue.use(). 例如:Vue.use(VueRouter).Vue.use(MintUI). 但是用 axios时,就不需要用 ...

  9. PHP实习生面试准备的建议

    你好,是我琉忆.PHP程序员面试笔试图书系列作者. 今天就跟大家聊聊作为一个PHP程序员,每年的跳槽季都应该怎么准备一番. 其实普遍的跳槽季总的就有2个. 分别是新年后的3-4月,还有9-10月份. ...

  10. Solution -「多校联训」取石子游戏

    \(\mathcal{Description}\)   Link.   有 \(n\) 堆石子,第 \(i\) 堆有 \(x_i\) 个,Alice 每次只能从这堆中拿走 \(a_i\) 个石子,Bo ...