leetcode 两个排序的中位数 python

两个排序数组的中位数

 

 

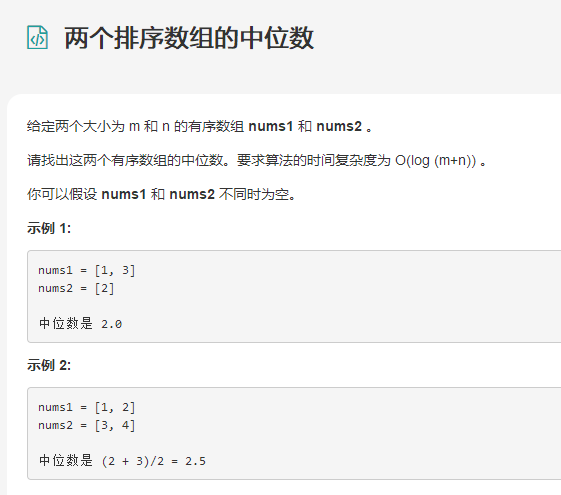
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2 。

请找出这两个有序数组的中位数。要求算法的时间复杂度为 O(log (m+n)) 。

你可以假设 nums1 和 nums2 不同时为空。

示例 1:

nums1 = [1, 3]
nums2 = [2]

中位数是 2.0

示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

中位数是 (2 + 3)/2 = 2.5

两个列表合并一下排个序， 然后再找中位数

　　奇数个元素就返回中间元素

　　偶数个元素返回中间两个的平均数

 class Solution:
     def findMedianSortedArrays(self, nums1, nums2):
         """
         :type nums1: List[int]
         :type nums2: List[int]
         :rtype: float
         """
         nums = nums1 + nums2
         nums.sort()
         l = len(nums)
         if l % 2 == 0:
             return (nums[int(l/2)] + nums[int(l/2-1)])/ 2
         else:
             return nums[int((l-1)/2)]