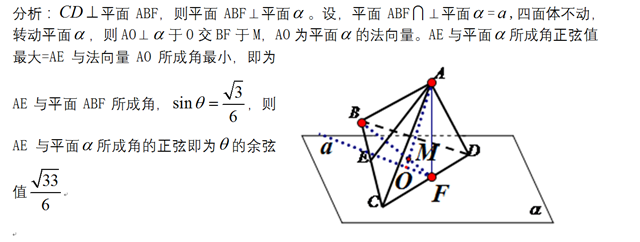
评：线面角最小，在此类最值中经常用到，作为选择填空可以投机.

MT【108】线面角最小的更多相关文章

  1. MT【118】利用线面角最小解题

    解:如图将正四面体放到立方体中,让AB通过$\alpha$面,让$\alpha$面绕着AB动起来.问题就转化成为EF与面$\alpha$线面角$\theta$了.EF的投影为$|EF|cos\thet ...

  2. MT【109】线面角最大时为二面角平面角

    解答:如图设C到$\alpha$面的距离为$d_1,C_1$到虚线距离为$d_2$ 所求距离$d=d_1+d_2=|AC|sin\theta+|CC_1|cos\theta=4\sqrt{2}sin\ ...

  3. MT【14】最大最小问题变形

    解答: 评:这类最大最小问题有几何方法和代数方法两种解法.

  4. MT【179】最大最小老问题

    求$\max\{x^2+2y+20,y^2-6x+12\}$的最小值______ 提示:$4t\ge 3(x^2+2y+20)+y^2-6x+12=3(x-1)^2+(y+3)^2+60\ge 60, ...

  5. MT【305】丹德林双球

    如图.在正方体$ABCD-A_1B_1C_1D_1$中,点$M,N$分别是直线$CD,AB$上的动点,点$P$是$\Delta A_1C_1D_1$内的动点(不包括边界),记直线$DP$与$MN$所成 ...

  6. MT【193】三面角的正余弦定理

    (原题为浙江名校新高考研究联盟2018届第三次联考选择压轴题) 在平面$\alpha$内,已知$AB\perp BC$,过直线$AB,BC$分别作平面$\beta,\gamma$,使得锐二面角$\al ...

  7. MT【52】空间法向量理解直线条数

    [从最简单的做起.]--波利亚 评:线面角转化成线与线的角,这道题还有类似的这类题是学生的难点.

  8. highstock K线图 深入研究

    K线图,相信每个股民都不陌生,如何用SVG画好一个K线图是一个难题. 我选择用highstock做为画图组件,适当的修改了一下源码,参考了数个财经网站的案例,完成了一个不太成熟的K线图,欢迎大家批评指 ...

  9. K-means的缺点（优化不仅仅是最小化误差）

    K-means的缺点(优化不仅仅是最小化误差) #转载时,请注明英文原作David Robinson,译者Ding Chao.# 我最近遇到一个交叉验证的问题,我认为这个给我提供了一个很好的机会去用“ ...

随机推荐

  1. 01-Maven功能特点

    1.Maven简介 2.Maven重要性 3.Maven原理

  2. 20155222卢梓杰 实验五 MSF基础应用

    实验五 MSF基础应用 1.一个主动攻击实践,如ms17_010_eternalblue漏洞; 本次攻击目标是win7虚拟机 首先进行相应配置 然后点launch 就成功了 针对win7的漏洞还是相对 ...

  3. Python中类和对象在内存中是如何保存？

    类以及类中的方法在内存中只有一份,而根据类创建的每一个对象都在内存中需要存一份,大致如下图: 如上图所示,根据类创建对象时,对象中除了封装 name 和 age 的值之外,还会保存一个类对象指针,该值 ...

  4. Visual Studio Package 插件开发(Visual Studio SDK)

    背景 这段时间公司新做了一个支付系统,里面有N个后台服务,每次有更新修改,拷贝打包发布包“不亦乐乎”...于是我想要不要自己定制个打包插件. 部分朋友可能会认为,有现成的可以去找一个,干嘛不用持续集成 ...

  5. markdown 笔记二

    Markdown 语法笔记==============================1,头部欢迎# 欢迎使用flaskBlog ------ flask对于我来说,适合快速开发一些小网页,自己也想整 ...

  6. React半科普文

    React半科普文 什么是React getting started 文件分离 Server端编译 定义一个组件 使用property 组件嵌套 组件更新 Virtual DOM react nati ...

  7. jmeter --http属性管理器

    1,http请求默认值 2,HTTP授权管理器 3,HTTP缓存管理 4,HTTP cookie 管理器 5,HTTP头文管理器

  8. TimelineJS JSON 数据格式 - 译文 [原创]

    TimelineJS 是用于绘制时间轴的 Javascript 开源脚本,目前是 TimelineJS3 版.参阅 https://github.com/NUKnightLab/TimelineJS3 ...

  9. LeetCode-37.解数独

    编写一个程序,通过已填充的空格来解决数独问题. 一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次. 数字 1-9 在每一列只能出现一次. 数字 1-9 在每一个以粗实线分隔的 3x3 ...

  10. B1004. 成绩排名

    这一题总算是把C++的重载活学活用了一回,节省了很多脑细胞. #include<bits/stdc++.h> using namespace std; struct student{ st ...