Trie树（c++实现）——转载自jihite的博客

Trie树（c++实现）

 

原理

先看个例子，存储字符串abc、ab、abm、abcde、pm可以利用以下方式存储

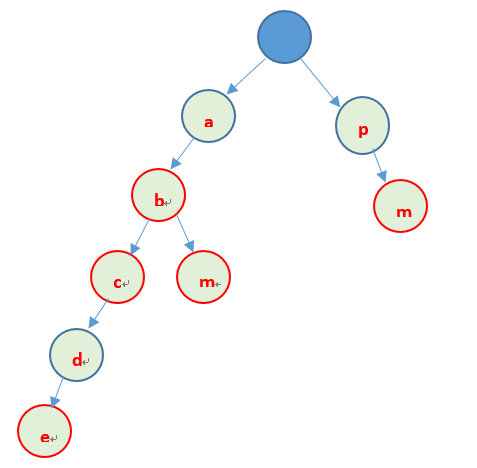
上边就是Trie树的基本原理：利用字串的公共前缀来节省存储空间，最大限度的减少无谓的字串比较。

应用

Trie树又称单词查找树，典型的应用是用于统计，排序和保存大量的字符串（不仅用于字符串），所以经常被搜索引擎系统用于文本词频的统计。

设计

trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

结点可以设计成这样：

class trieNode
{
    public:
        trieNode() : terminableSize(), nodeSize() { for(int i = ; i < Size; ++i) children[i] = NULL; }
        ~trieNode()
        {
            for(int i = ; i < Size; ++i)
            {
                delete children[i];
                children[i] = NULL;
            }
        }
    public:
        int terminableSize;          //存储以此结点为结尾的字串的个数
        int nodeSize;                //记录此结点孩子的个数
        trieNode* children[Size];    //该数组记录指向孩子的指针
};

图示

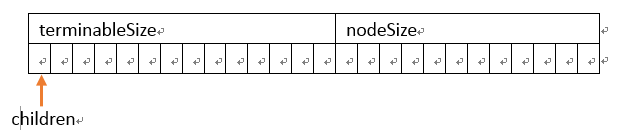
树设计成这样：

template<int Size, class Type>
class trie
{
    public:
        typedef trieNode<Size> Node;
        typedef trieNode<Size>* pNode;
        trie() : root(new Node) {}

        template<class Iterator>
        void insert(Iterator beg, Iterator end);
        void insert(const char *str);

        template<class Iterator>
        bool find(Iterator beg, Iterator end);
        bool find(const char *str);

        template<class Iterator>
        bool downNodeAlone(Iterator beg);

        template<class Iterator>
        bool erase(Iterator beg, Iterator end);
        bool erase(const char *str);

        int sizeAll(pNode);
        int sizeNoneRedundant(pNode);
    public:
        pNode root;
    private:
        Type index;
};

index字串索引利用（char % 26） 得到，这样'a' % 26 = 19, 'b' % 26 = 20

实现

插入

以插入abc、ab为例

]

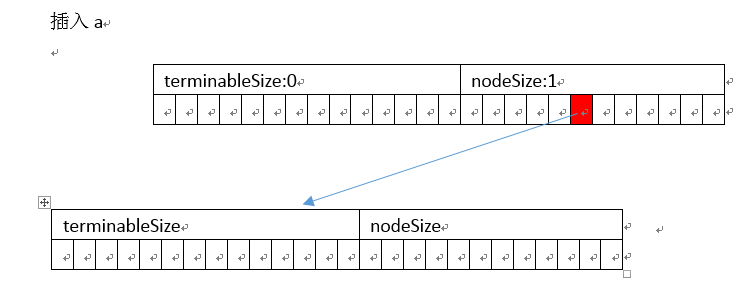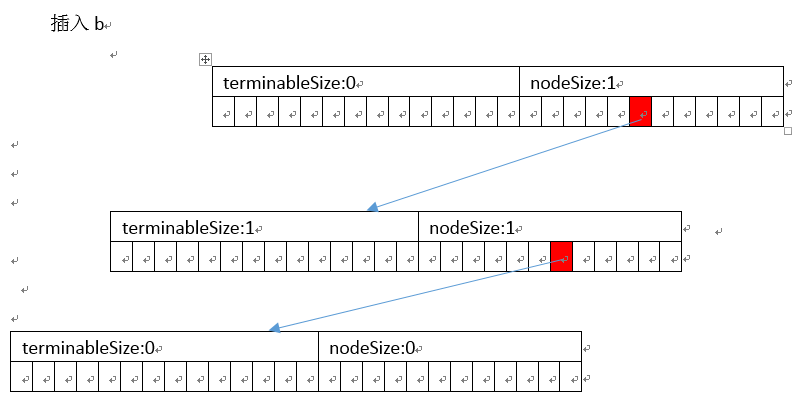
删除

删除结点，首先查找此字串是否在树中，如果在树中，再查找此结点以下的部分是不是都是只有一个孩子，并且每个结点只有叶子结点是结束结点，如果不是继续往下重复上边过程。

统计字串个数

分两种情况

1. 计算重复的字串的个数：是结束结点，此时加的是terminabel的个数
2. 计算不重复的字串的个数：是结束结点，此时加的是1(当terminabel>0）的个数

参考代码

#include <iostream>
#include <cstring>
using namespace std;

template<int Size>
class trieNode
{
    public:
        trieNode() : terminableSize(), nodeSize() { for(int i = ; i < Size; ++i) children[i] = NULL; }
        ~trieNode()
        {
            for(int i = ; i < Size; ++i)
            {
                delete children[i];
                children[i] = NULL;
            }
        }
    public:
        int terminableSize;
        int nodeSize;
        trieNode* children[Size];
};

template<int Size, class Type>
class trie
{
    public:
        typedef trieNode<Size> Node;
        typedef trieNode<Size>* pNode;
        trie() : root(new Node) {}

        template<class Iterator>
        void insert(Iterator beg, Iterator end);
        void insert(const char *str);

        template<class Iterator>
        bool find(Iterator beg, Iterator end);
        bool find(const char *str);

        template<class Iterator>
        bool downNodeAlone(Iterator beg);

        template<class Iterator>
        bool erase(Iterator beg, Iterator end);
        bool erase(const char *str);

        int sizeAll(pNode);
        int sizeNoneRedundant(pNode);
    public:
        pNode root;
    private:
        Type index;
};

template<int Size, class Type>
template<class Iterator>
void trie<Size, Type>::insert(Iterator beg, Iterator end)
{
    pNode cur = root;
    pNode pre;
    for(; beg != end; ++beg)
    {
        if(!cur->children[index[*beg]])
        {
            cur->children[index[*beg]] = new(Node);
            ++cur->nodeSize;
        }
        pre = cur;
        cur = cur->children[index[*beg]];
    }
    ++pre->terminableSize;
}
template<int Size, class Type>
void trie<Size, Type>::insert(const char *str)
{
    return insert(str, str + strlen(str));
}

template<int Size, class Type>
template<class Iterator>
bool trie<Size, Type>::find(Iterator beg, Iterator end)
{
    pNode cur = root;
    pNode pre;
    for(; beg != end; ++beg)
    {
        if(!cur->children[index[*beg]])
        {
            return false;
            break;
        }
        pre = cur;
        cur = cur->children[index[*beg]];
    }
    if(pre->terminableSize > )
        return true;
    return false;
}

template<int Size, class Type>
bool trie<Size, Type>::find(const char *str)
{
    return find(str, str + strlen(str));
}

template<int Size, class Type>
template<class Iterator>
bool trie<Size, Type>::downNodeAlone(Iterator beg)
{
    pNode cur = root;
    int terminableSum = ;
    while(cur->nodeSize != )
    {
        terminableSum += cur->terminableSize;
        if(cur->nodeSize > )
            return false;
        else          //cur->nodeSize = 1
        {
            for(int i = ; i < Size; ++i)
            {
                if(cur->children[i])
                    cur = cur->children[i];
            }
        }
    }
    if(terminableSum == )
        return true;
    return false;
}
template<int Size, class Type>
template<class Iterator>
bool trie<Size, Type>::erase(Iterator beg, Iterator end)
{
    if(find(beg, end))
    {
        pNode cur = root;
        pNode pre;
        for(; beg != end; ++beg)
        {
            if(downNodeAlone(cur))
            {
                delete cur;
                return true;
            }
            pre = cur;
            cur = cur->children[index[*beg]];
        }
        if(pre->terminableSize > )
            --pre->terminableSize;
        return true;
    }
    return false;
}

template<int Size, class Type>
bool trie<Size, Type>::erase(const char *str)
{
    if(find(str))
    {
        erase(str, str + strlen(str));
        return true;
    }
    return false;
}

template<int Size, class Type>
int trie<Size, Type>::sizeAll(pNode ptr)
{
    if(ptr == NULL)
        return ;
    int rev = ptr->terminableSize;
    for(int i = ; i < Size; ++i)
        rev += sizeAll(ptr->children[i]);
    return rev;
}

template<int Size, class Type>
int trie<Size, Type>::sizeNoneRedundant(pNode ptr)
{
    if(ptr == NULL)
        return ;
    int rev = ;
    if(ptr->terminableSize > )
        rev = ;
    if(ptr->nodeSize != )
    {
        for(int i = ; i < Size; ++i)
            rev += sizeNoneRedundant(ptr->children[i]);
    }
    return rev;
}

template<int Size>
class Index
{
    public:
        int operator[](char vchar)
        { return vchar % Size; }
};

int main()
{
    trie<, Index<> > t;
    t.insert("hello");
    t.insert("hello");
    t.insert("h");
    t.insert("h");
    t.insert("he");
    t.insert("hel");
    cout << "SizeALL:" << t.sizeAll(t.root) << endl;
    cout << "SizeALL:" << t.sizeNoneRedundant(t.root) << endl;
    t.erase("h");
    cout << "SizeALL:" << t.sizeAll(t.root) << endl;
    cout << "SizeALL:" << t.sizeNoneRedundant(t.root) << endl;
}

 结果 

 技术实现细节

1. 对树的删除，并不是树销毁结点，而是通过结点自身的析构函数实现

2. 模版类、模版函数、非类型模版可以参考：http://www.cnblogs.com/kaituorensheng/p/3601495.html

3. 字母的存储并不是存储的字母，而是存储的位置，如果该位置的指针为空，则说明此处没有字母；反之有字母。

4. terminableNum存储以此结点为结束结点的个数，这样可以避免删除时，不知道是否有多个相同字符串的情况。

 

 

——转载自jihite的博客