Hanoi II——汉诺塔步数求解进阶问题

在NOJ上遇到关于汉诺塔步数的求解问题

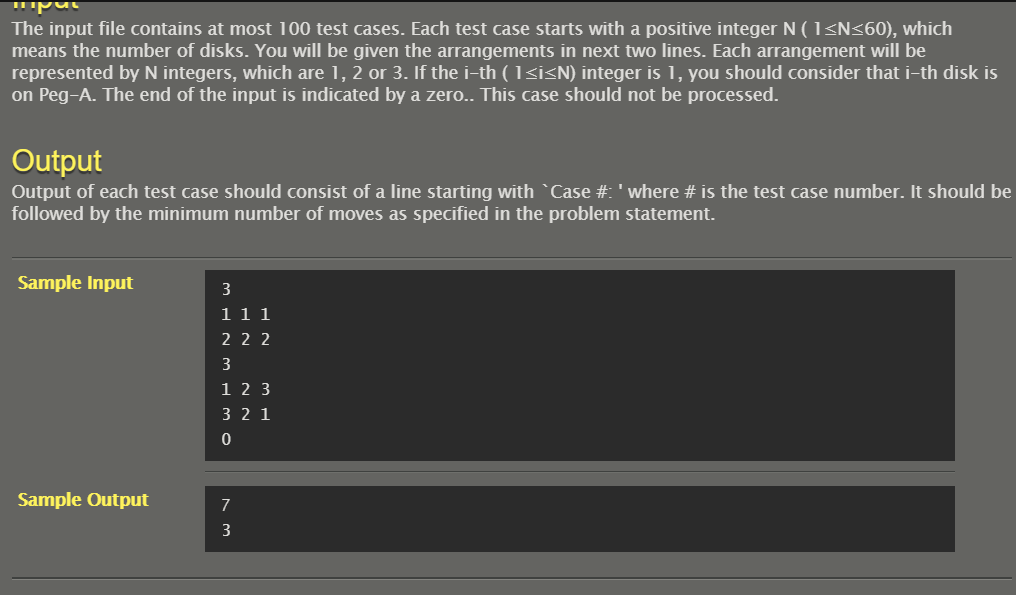
开始读时一脸懵逼，甚至不知道输入的数据是什么意思

题目描述：给出汉诺塔的两个状态，从初始状态移动到目的状态所需要的最少步数

对于初级汉诺塔步数问题，我们可以直接通过公式进行求解，概括来说，从一个柱子到另一个柱子移动n个盘子，需要2的n次方-1步

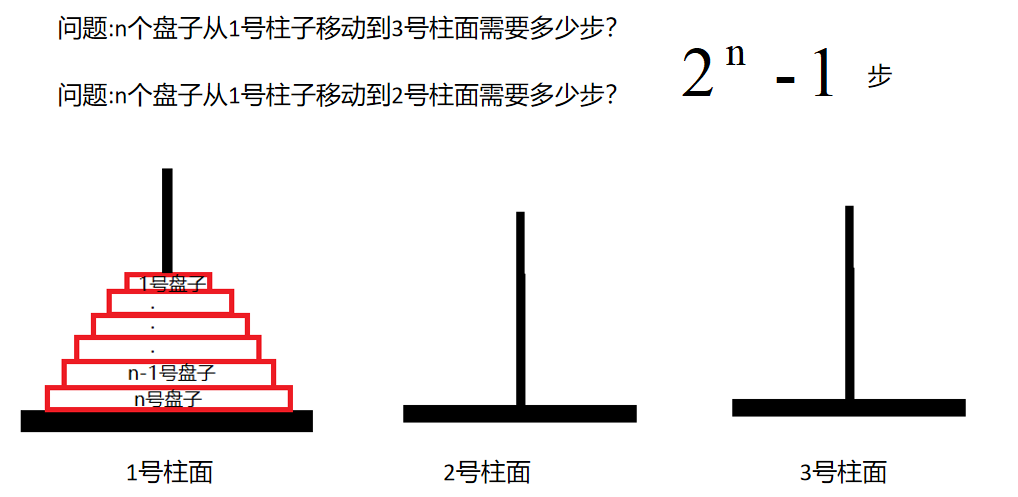
下面看一下输入的是什么数据，通过一个例子进行说明

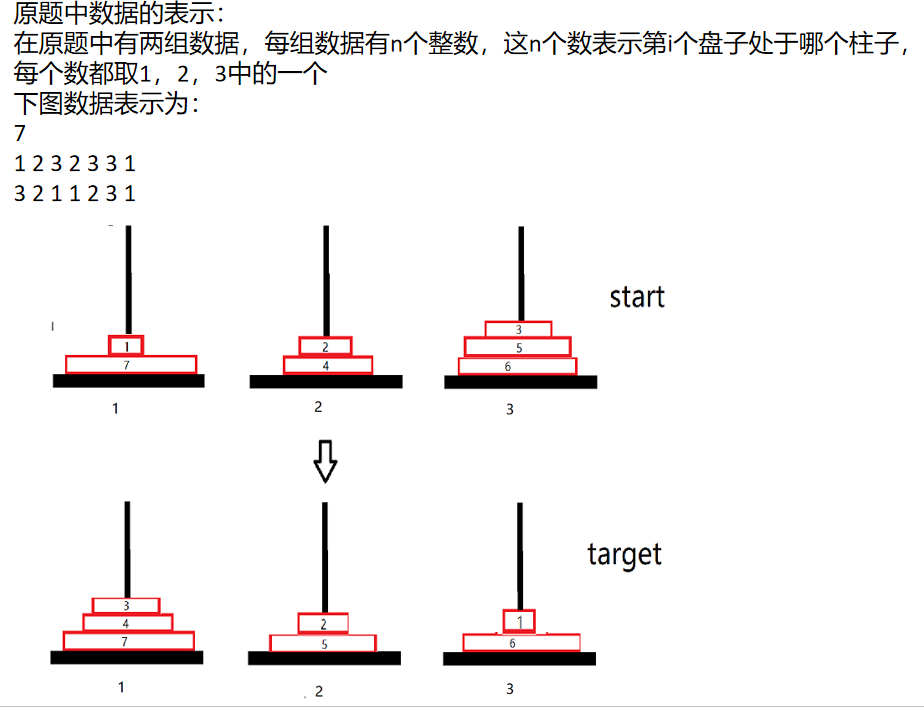
下面看问题的求解

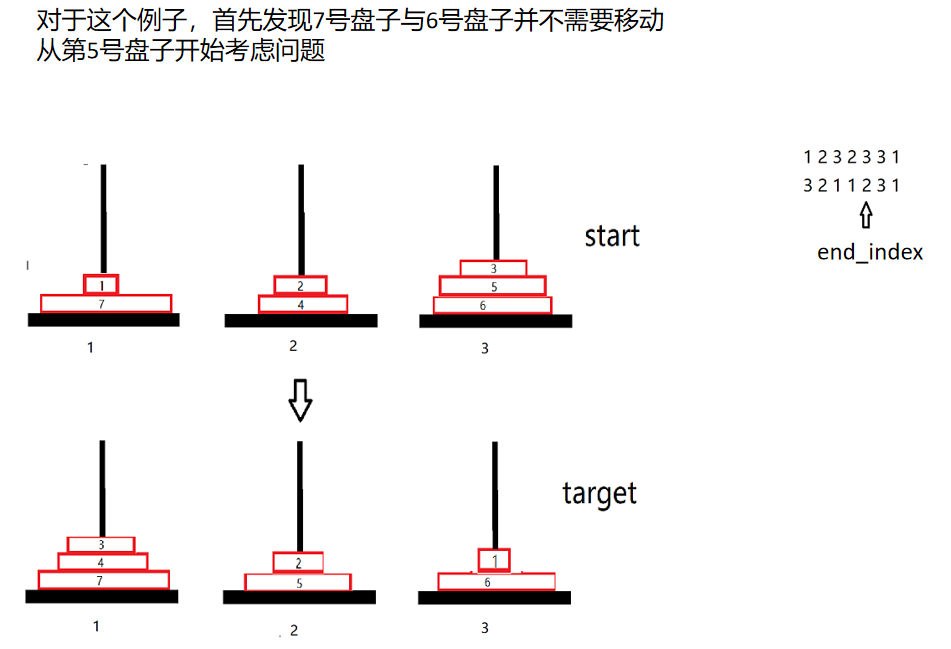
对题目的分析就到这，下面给出具体的程序：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
long long fun(int *num,int i,int f)
{
    if(i<)return ;
    if(num[i]==f)return fun(num,i-,f);
    return fun(num,i-,-num[i]-f)+(1LL<<(i-));
}
int main()
{
    long long ans;
    int n;
    int start[],target[];
    while(scanf("%d",&n))
    {
        if(n==)break;
        for(int i = ;i<=n;i++)scanf("%d",&start[i]);
        for(int i = ;i<=n;i++)scanf("%d",&target[i]);
        int index_end = n;
        ans = ;
        while(index_end>= && start[index_end]==target[index_end]){
            index_end--;
        }
        if(index_end==){
            printf("0\n");
            continue;
        }else{
            int other = -start[index_end]-target[index_end];
            ans = fun(start,index_end-,other)+fun(target,index_end-,other)+;
            printf("%lld\n",ans);
        }

    }

    return ;
}

第一次博客园的总结就这到这啦

如果大家有疑问可以留言讨论