洛谷 P3382 【模板】三分法(三分 二分)

P3382 【模板】三分法

题目提供者HansBug

难度 普及/提高-

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。



输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

输入样例#1：

3 -0.9981 0.5

1 -3 -3 1

输出样例#1：

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

样例说明：

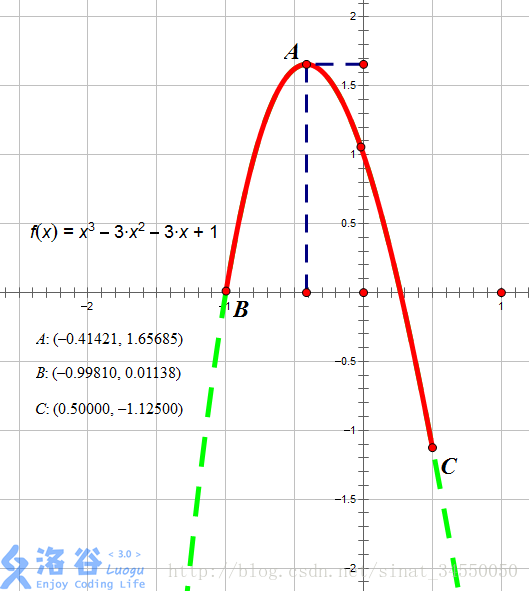
如图所示，红色段即为该函数f(x)=x^3-3x^2-3x+1在区间[-0.9981,0.5]上的图像。

当x=-0.41421时图像位于最高点，故此时函数在[l,x]上单调增，[x,r]上单调减，故x=-0.41421，输出-0.41421。

/*
三分答案做法.
又学了一种三分答案姿势.
mid=(2*l+r)/3,midmid=(l+2*r)/3.
常数要小很多...
(并不会证明).
*/
#include<cstdio>
#define MAXN 101
#define eps 1e-7
using namespace std;
double a[MAXN],ans,l,r;
int n;
double check(double x)
{
    double sum=0;
    for(int i=1;i<=n;i++)
    {
        double tot=a[i];
        for(int j=1;j<=n-i;j++) tot*=x;
        sum+=tot;
    }
    return sum;
}
void sanfen()
{
    double mid,midmid;
    while(l+eps<r)
    {
        //mid=(l+r)/2,midmid=(mid+r)/2;
        mid=(2*l+r)/3,midmid=(l+2*r)/3;
        if(check(mid)>=check(midmid)) r=midmid,ans=mid;
        else l=mid;
    }
    printf("%.5f",ans);
    return ;
}
int main()
{
    scanf("%d",&n);
    scanf("%lf%lf",&l,&r);n++;
    for(int i=1;i<=n;i++) scanf("%lf",&a[i]);
    sanfen();
    return 0;
}

/*
二分答案.
对函数求导,找f`(x)=0的点.
感觉这题数据应该都是单峰函数.
so 这个方法就ok了.
其实应该还要判断该点两侧导函数是否变号
还有带入端点值比较啥的.
懒没写~.
重要的是昨天刚预习的高二导数求凸形函数
今天就用上了 先让我笑一会儿哈哈哈哈哈哈哈.
*/
#include<iostream>
#include<cstdio>
#define eps 1e-7
#define MAXN 101
using namespace std;
double a[MAXN],ans,l,r;
int n;
double check(double x)
{
    double sum=0;
    for(int i=1;i<=n;i++)
    {
        double tot=a[i]*(n-i+1);
        for(int j=1;j<=n-i;j++) tot*=x;
        sum+=tot;
    }
    return sum;
}
void erfen()
{
    double mid;
    while(l+eps<r)
    {
        mid=(l+r)/2;
        if(check(mid)<=0) r=mid,ans=mid;
        else l=mid;
    }
    printf("%.5f",ans);
    return ;
}
int main()
{
    scanf("%d",&n);
    scanf("%lf%lf",&l,&r);n++;
    for(int i=1;i<=n;i++) scanf("%lf",&a[i]);n--;
    erfen();
    return 0;
}