matlab学习——02整数规划(蒙特卡洛法,指派问题，混合整数规划)

02整数规划

蒙特卡洛法(随机取样法)

编写文件mengte.m，目标函数f和约束向量g

function[f,g]=mengte(x);
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-...
    2*x(5);
g=[
    sum(x)-400
    x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
    2*x(1)+x(2)+6*x(3)-200
    x(3)+x(4)+5*x(5)-200
    ];　

主函数

format compact;
rand('state',sum(clock)); % 初始化随机数发生器
p0=0;
tic % 计时开始
for i=1:10^6
    x=randi([0,99],1,5); % 产生1行5列的区间[0,99]上的随机整数
    [f,g]=mengte(x);
    if all(g<=0)
        if p0<f
            x0=0;p0=f; % 记录下当前较好的解
        end
    end
end
x0,p0
toc % 计时结束

指派问题

clear
C=[2	10	9	7
15	4	14	8
13	14	16	11
4	15	13	9];

A = perms(1:4);%perm显示1，2，3，4四个数的全排列
L = length(A)
for i=1:L
    a = zeros(4,4);
    b = A(i,:);%遍历全排列中的每一种
    c = 1:4;
    a(sub2ind(size(a), b, c))=1;%a矩阵指定的位置赋值为1
    D{i}=a;
    S(i)=sum(sum(a.*C));%求出费用和
end
[a,b]=find(S==min(S))
D{b}
S(b)

%适用于任意n阶系数矩阵
clear all；
C=[2	10	9	7,
15	4	14	8,
13	14	16	11,
4	15	13	9,
];%效率矩阵C
n=size(C,1);%计算C的行列数n
C=C(:);%计算目标函数系数，将矩阵C按列排成一个列向量即可。
A=[];B=[];%没有不等式约束
Ae=zeros(2*n,n^2);%计算等约束的系数矩阵a
for i=1:n
    for j=(i-1)*n+1:n*i
        Ae(i,j)=1;
    end
    for k=i:n:n^2
        Ae(n+i,k)=1;
    end
end
Be=ones(2*n,1);%等式约束右端项b
Xm=zeros(n^2,1);%决策变量下界Xm
XM=ones(n^2,1);%决策变量上界XM
[x,z]=linprog(C,A,B,Ae,Be,Xm,XM);%使用linprog求解
x=reshape(x,n,n);%将列向量x按列排成一个n阶方阵
disp('最优解矩阵为:');%输出指派方案和最优值
Assignment=round(x)%使用round进行四舍五入取整
disp('最优解为:');
z

　

混合整数规划

format compact
% min z = -3x1-2x2-x3
% x1+x2+x3 <=7
% 4x1+2x2+x3=12
% x1,x2>=0
% x3=0或1

clc,clear
f=[-3;-2;-1];intcon=3; % 整数变量的地址
a=ones(1,3);b=7;
aeq=[4 2 1];beq=12;
lb=zeros(3,1);ub=[inf;inf;1]; % x(3)为0-1变量
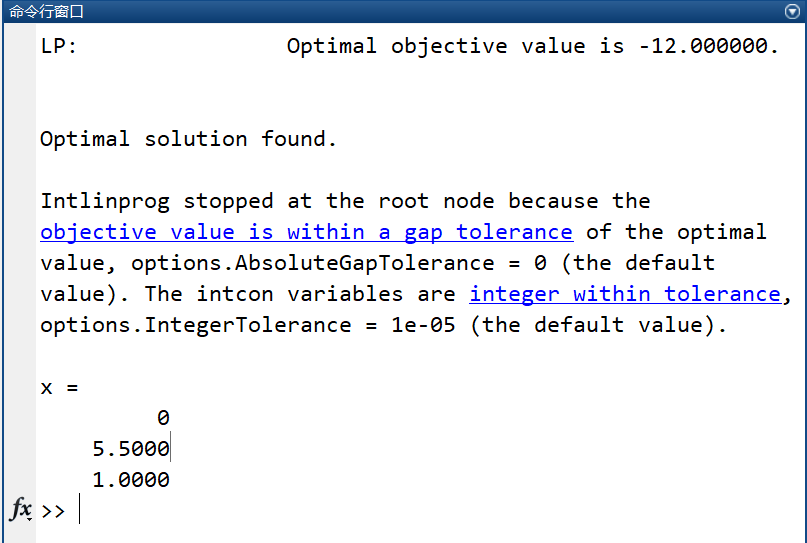
x=intlinprog(f,intcon,a,b,aeq,beq,lb,ub)