sift-高斯金字塔

一、高斯金字塔

金字塔的层是由降采样得到的，而每一层又有多张图像，其他的图像是由初始的一张经过高斯模糊的得到的。

注意的是：高斯金字塔有层，而金字塔的每一层有一组图像，这一组图像也形成了层。注意两个层的区别。

1、降采样时，高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。

2、为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如图3.1所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊，使得金字塔的每层含有多张高斯模糊图像，这也就是每一组有多层的原因了（当前组的其他图像是根据【1】那张图像进行高斯模糊得到。以此类推）

3、每一组有几层图像（组：金字塔的层）

金字塔层数（组）计算公式：

其中M，N为原图像的大小,t为塔顶图像的最小维数的对数值（对数底为2）。

二、高斯差分金字塔

1、起源：

　　2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数的极大值和极小值同其它的特征提取函数，例如：梯度，Hessian或Harris角特征比较，能够产生最稳定的图像特征。

而Lindeberg早在1994年就发现高斯差分函数（Difference of Gaussian ，简称DOG算子）与尺度归一化的高斯拉普拉斯函数非常近似。因此就用差分逼近，从而叫做高斯差分金字塔。
2、公式：

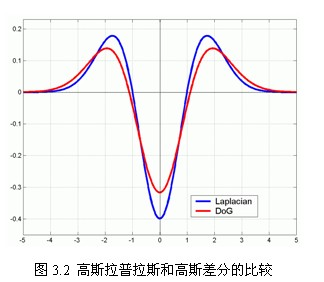
3、使用高斯金字塔每组中相邻上下两层图像相减，得到高斯差分图像

关键点是由DOG空间的局部极值点组成的。假如每组含4层的高斯差分金子塔，只能在中间两层中进行两个尺度的极值点检测，其它尺度则只能在不同组中进行。为了在每组中检测S个尺度的极值点，则DOG金字塔每组需S+2层图像，而DOG金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需S+3层图像，实际计算时S在3到5之间。

4、在最开始建立高斯金字塔时，要预先模糊输入图像来作为第0个组的第0层的图像，这时相当于丢弃了最高的空域的采样率。因此通常的做法是先将图像的尺度扩大一倍来生成第-1组。我们假定初始的输入图像为了抗击混淆现象

5、离散空间的极值点并不是真正的极值点（因为采样的过程中丢失了一些信息）：利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值（注：具体方法我还没有理解清楚）

三、关键点方向分配

　　为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个基准方向。使用图像梯度的方法求取局部结构的稳定方向。对于在DOG金字塔中检测出的关键点点，采集其所在高斯金字塔图像3σ邻域窗口内像素的梯度和方向分布特征。梯度的模值和方向如下：

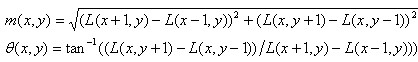
采用直方图来统计梯度和方向：类似hog

直方图的峰值方向代表了关键点的主方向

将检测出的含有位置、尺度和方向的关键点即是该图像的SIFT特征点。

四、SIFT的缺点

SIFT在图像的不变特征提取方面拥有无与伦比的优势，但并不完美，仍然存在：

1. 实时性不高。

2. 有时特征点较少。

3. 对边缘光滑的目标无法准确提取特征点。

大致了解了sift，至于有些细节还不能很好的学习到。

参考：https://blog.csdn.net/zddblog/article/details/7521424