opencv —— boundingRect、minAreaRect 寻找包裹轮廓的最小正矩形、最小斜矩形

寻找包裹轮廓的最小正矩形：boundingRect 函数

返回矩阵应满足：① 轮廓上的点均在矩阵空间内。② 矩阵是正矩阵（矩形的边界与图像边界平行）。

Rect boundingRect(InputArray points);

• 唯一一个参数是输入的二维点集，可以是 vector 或 Mat 类型。

代码示例：

#include<opencv.hpp>
#include<iostream>
using namespace cv;
using namespace std;
int main(){
    Mat src = imread("C:/Users/齐明洋/Desktop/7.jpg");
    imshow("src", src);

    Mat gray, bin_img;
    cvtColor(src, gray, COLOR_BGR2GRAY);   //将原图转换为灰度图
    imshow("gray", gray);

    //二值化
    threshold(gray, bin_img, , , THRESH_BINARY_INV);
    imshow("bin_img", bin_img);

    //寻找最外围轮廓
    vector<vector<Point> >contours;
    findContours(bin_img, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);

    //绘制边界矩阵
    RNG rngs = {  };
    Mat dst = Mat::zeros(src.size(), src.type());
    for (int i = ; i < contours.size(); i++) {
        Scalar colors = Scalar(rngs.uniform(, ), rngs.uniform(, ), rngs.uniform(, ));
        drawContours(dst, contours, i, colors, );
        Rect rects = boundingRect(contours[i]);
        rectangle(dst, rects, colors, );
    }
    imshow("dst", dst);

    waitKey();
}

效果演示：

寻找包裹轮廓的最小斜矩形：minAreaRect 函数

返回矩阵应满足：① 轮廓上的点均在矩阵空间内。② 没有面积更小的满足条件的矩阵（与 boundingRect 返回结果的区别是：矩形的边界不必与图像边界平行）。

需要补充的是，求点集的拟合椭圆（fitEllipse() https://www.cnblogs.com/bjxqmy/p/12354750.html）便是求斜矩阵内最大的椭圆（矩阵长宽分别做椭圆长轴、短轴）。

RotatedRect minAreaRect(InputArray points);

• 唯一一个参数是输入的二维点集，可以是 vector 或 Mat 类型。

代码示例：

#include<opencv.hpp>
#include<iostream>
#include<vector>
using namespace cv;
using namespace std;
int main() {
    Mat src = imread("C:/Users/齐明洋/Desktop/7.jpg");
    imshow("src", src);

    Mat gray, bin_img;
    cvtColor(src, gray, COLOR_BGR2GRAY);   //将原图转换为灰度图
    imshow("gray", gray);

    //二值化
    threshold(gray, bin_img, , , THRESH_BINARY_INV);
    imshow("bin_img", bin_img);

    //寻找最外围轮廓
    vector<vector<Point> >contours;
    findContours(bin_img, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);

    //绘制最小边界矩阵
    RNG rngs = {  };
    Mat dst = Mat::zeros(src.size(), src.type());
    Point2f pts[];
    for (int i = ; i < contours.size(); i++) {
        Scalar colors = Scalar(rngs.uniform(, ), rngs.uniform(, ), rngs.uniform(, ));
        drawContours(dst, contours, i, colors, );
        RotatedRect rects = minAreaRect(contours[i]);
        rects.points(pts);//确定旋转矩阵的四个顶点
        for (int i = ; i < ; i++) {
            line(dst, pts[i], pts[(i + ) % ], colors, );
        }
    }
    imshow("dst", dst);

    waitKey();
}

效果演示：

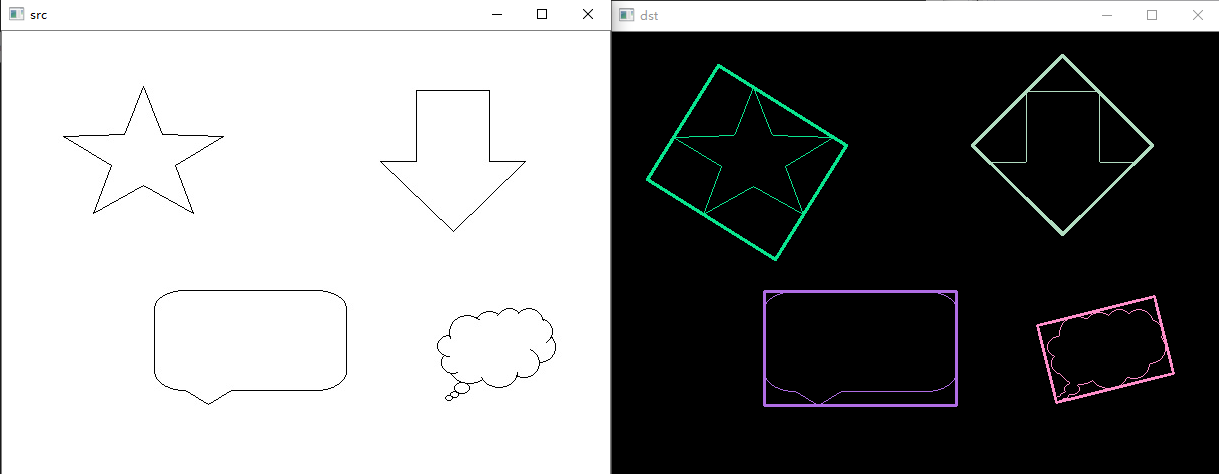
借鉴博客：https://www.cnblogs.com/little-monkey/p/7429579.html

http://www.pianshen.com/article/4286104294/