选择合适的最短路--hdu3499

[题目链接](http://acm.hdu.edu.cn/showproblem.php?pid=3499)

刚看见题目，哦？不就是个最短路么，来，跑一下dijkstra记录最长路除个二就完事了 ，但是。。。。。。

走红色的路是最佳方案，但是蓝色路的最短路跟短，我想错了；

不久我又想，把每个边枚举一下，减半一个边，就跑一次dijstra，但是这太慢了，O(m*m*logm)

拜拜了您內

后来看了看网上的大佬，其实也可以枚举嘛，只要每一次枚举都是O（1）。显然需要预处理一下，正线边跑一次，反向边跑一次

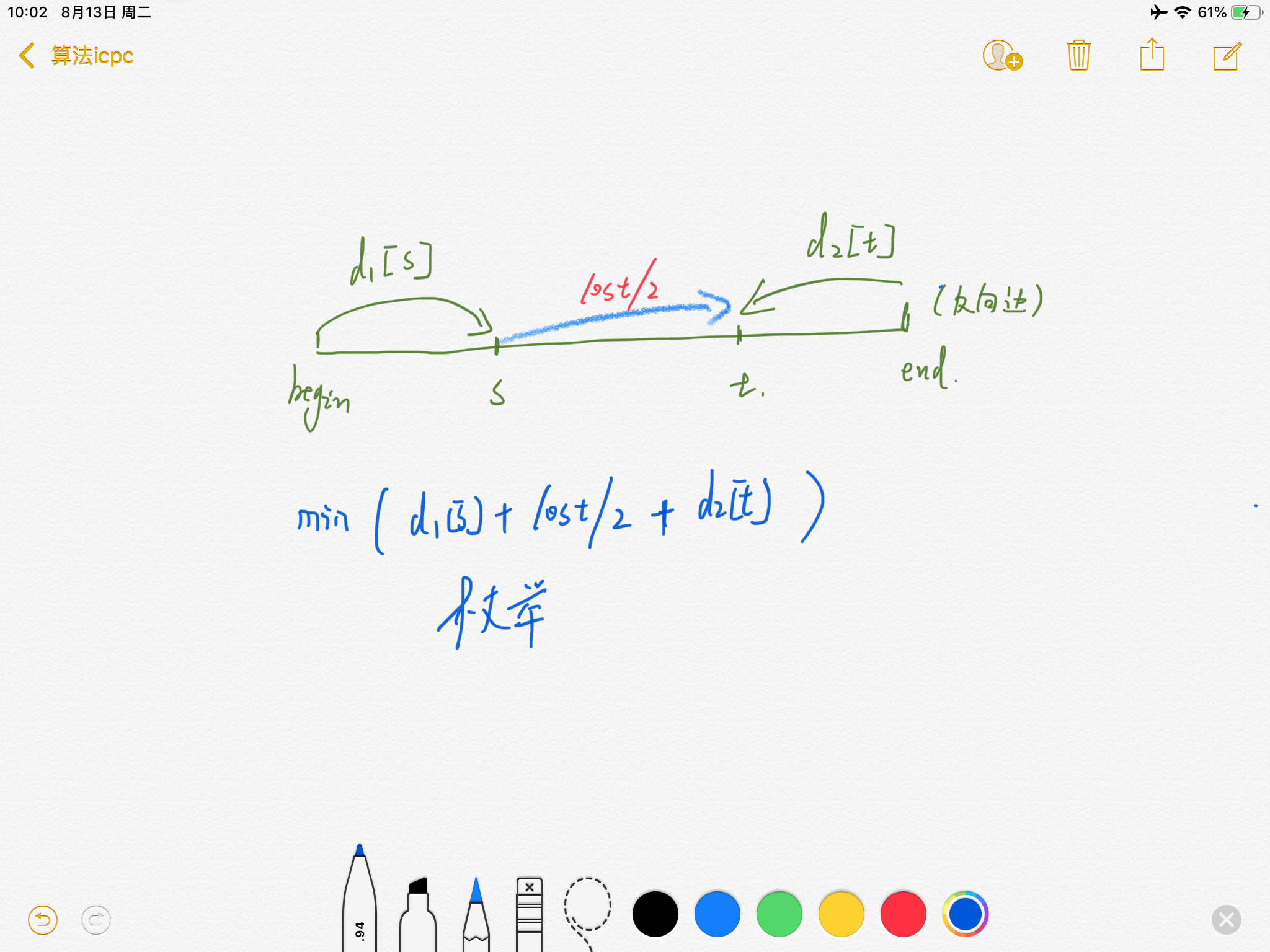
这样就可以了

听说还可以分层图，没看懂，猜测了一下原理

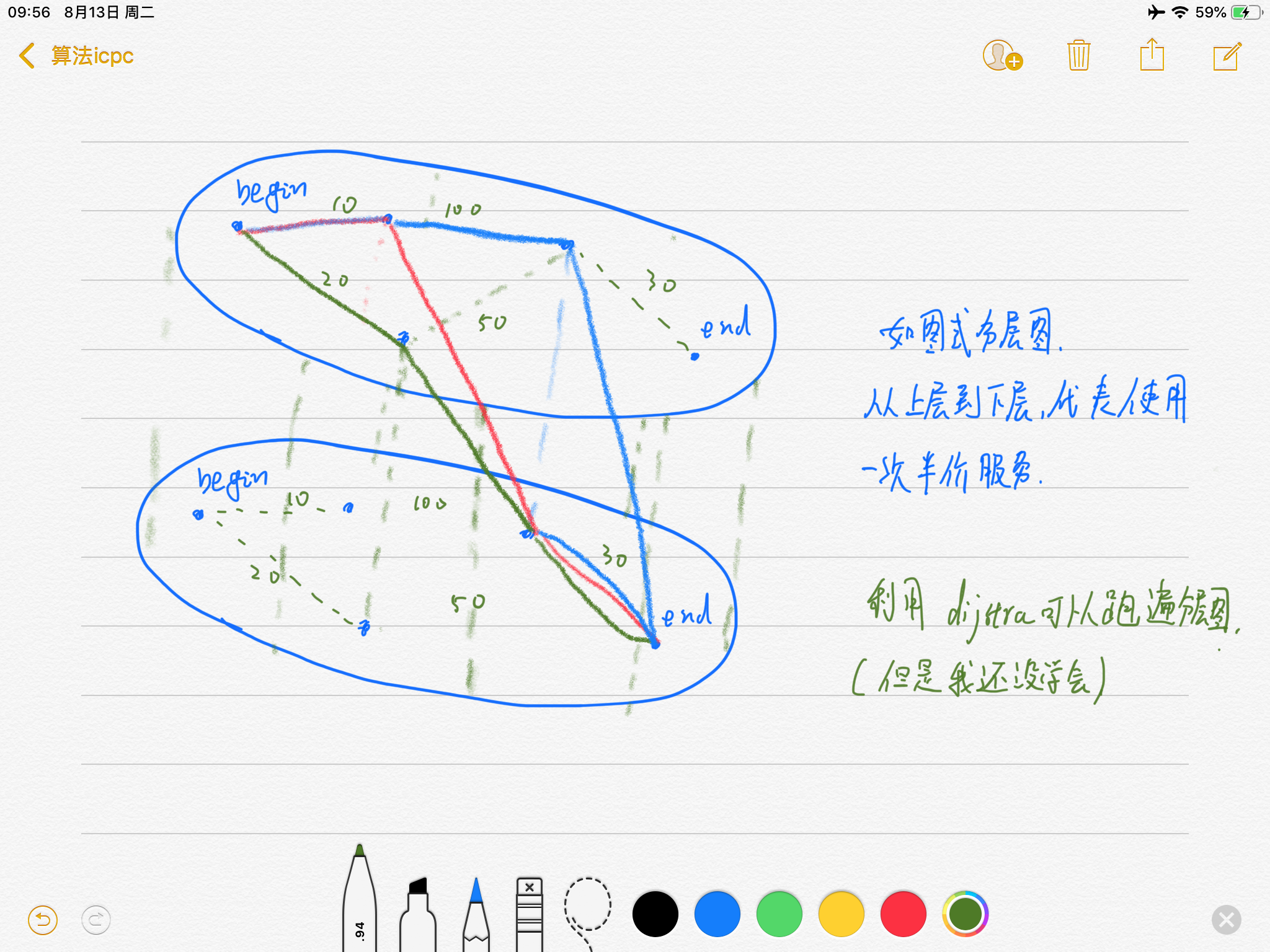
就这样了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
#include<map>
#include<string>
using namespace std;
typedef long long ll;
const int maxn = 5e5 + 100;
const long long INF = 1e12;
struct Node {
	ll p, val;
	Node(ll a, ll b) :p(a), val(b) {}
};
bool operator <(const Node a, const Node b) {
	if (a.val > b.val) return true;
	else return false;
}
int n, m;
ll d1[maxn];
ll d2[maxn];
int vis[maxn];
vector<Node>G[maxn];
void insert(int be, int en, int len) {
	G[be].push_back(Node(en, len));
	return;
}
int dijstra(ll *dis, int be) {
	for (int i = 0; i <= n; i++) {
		vis[i] = 0;
		dis[i] = INF;
	}
	dis[be] = 0;
	priority_queue<Node>que;
	que.push(Node(be, 0));
	while (!que.empty()) {
		Node ans = que.top();
		que.pop();
		if (vis[ans.p] == 0) {
			vis[ans.p] = 1;
			for (int i = 0; i < G[ans.p].size(); i++) {
				int p = G[ans.p][i].p;
				if (!vis[p] && dis[p] > dis[ans.p] + G[ans.p][i].val) {
					dis[p] = dis[ans.p] + G[ans.p][i].val;
					que.push(Node(p, dis[p]));
				}
			}
		}
	}
	return 0;
}
map<string, int>ins;
ll be_[maxn];
ll en_[maxn];
ll len_[maxn];
int main() {
	while (~scanf("%d %d", &n, &m)) {
		ins.clear();//可得记得清空啊
		string be, en;
		ll len = 0;
		int c = 0;
		int cnt = 1;
		while (m--) {
			cin >> be >> en;
			scanf("%lld", &len);
			if (ins[be] == 0) ins[be] = cnt++;
			if (ins[en] == 0) ins[en] = cnt++;
			be_[c] = ins[be];
			en_[c] = ins[en];
			len_[c] = len;
			c++;
			insert(ins[en], ins[be], len);
		}
		cin >> be >> en;
		if (ins[be] == 0) ins[be] = cnt++;
		if (ins[en] == 0) ins[en] = cnt++;
		dijstra(d2, ins[en]);
		for (int i = 0; i <= n; i++) G[i].clear();
		for (int i = 0; i < c; i++) {
			insert(be_[i], en_[i], len_[i]);
		}
		dijstra(d1, ins[be]);
		ll ans = d1[ins[en]];
		if (ans == INF) {
			printf("-1\n");
			continue;
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 0; j < G[i].size(); j++) {
				ans = min(ans, d1[i] + d2[G[i][j].p] + G[i][j].val / 2);//每个顶点刷出来边试探
			}
		}

		printf("%lld\n", ans);
		for (int i = 0; i <= n; i++) G[i].clear();
	}
	return 0;
}