【剑指offer】数组中的逆序对。C++实现

原创文章，转载请注明出处！

博客文章索引地址

博客文章中代码的github地址

# 题目

# 思路

基于归并排序的思想统计逆序对：先把数组分割成子数组，再子数组合并的过程中统计逆序对的数目。统计逆序对时，先统计子数组内部的逆序对的数目，再统计相邻子数组的逆序对数目。

1.基于归并思想统计逆序对的过程

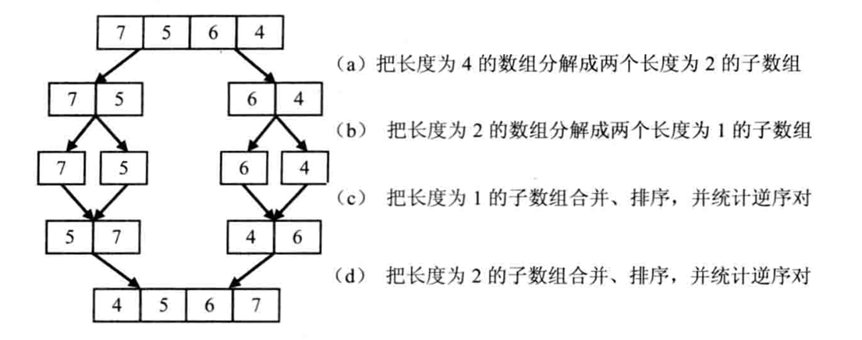
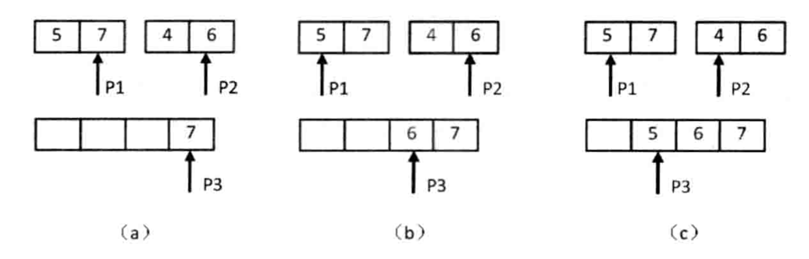
2.合并子数组统计逆序对的过程

      把长度为2的子数组合并、排序并统计逆序对的过程。

# 代码

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出, 即输出P%1000000007。题目保证输入的数组中没有过相同的数字。

  1 #include <iostream>
  2 #include <vector>
  3 using namespace std;
  4
  5 class Solution{
  6 public:
  7     int count=0;
  8     int InversePairs(vector<int> data)
  9     {
 10         // 检查边界条件
 11         if(data.size() != 0)
 12         {
 13             MergeSort(data,0,data.size()-1);
 14         }
 15         return count;
 16     }
 17
 18 private:
 19     void MergeSort(vector<int> a, int l, int r)
 20     {
 21         /* 将长度为n的输入序列分成两个长度为n/2的子序列 */
 22         if (l < r)
 23         {
 24             /* 中间元素*/
 25             int m = (l + r) >>1;
 26
 27             // 递归拆分
 28             MergeSort(a, l, m);
 29             MergeSort(a, m + 1, r);
 30
 31             // 递归合并
 32             Merge(a, l, m, r);
 33         }
 34     }
 35     void Merge(vector<int> a, int l, int m, int r)
 36     {
 37         vector<int> t;
 38         //int p = 0;    /* p指向辅助数组 */
 39         int i = l;    /* i指向第一个子表 */
 40         int j = m + 1;/* j指向第二个子表 */
 41
 42         /* 两个子表都不为空时 */
 43         while(i <= m && j <= r)
 44         {
 45             /* 取关键字小的元素转移至临时数组 */
 46             if (a[i] > a[j])
 47             {
 48                 t.push_back(a[j++]);
 49                 count=(count+m-i+1)%1000000007;
 50             }
 51             else
 52                 t.push_back(a[i++]);
 53         }
 54
 55         while(i <= m) t.push_back(a[i++]);/* 将非空的输入区间转移至输出区间 */
 56         while(j <= r) t.push_back(a[j++]);
 57
 58         for (i = 0; i < t.size(); i++) a[l + i] = t[i];/* 归并完成后将结果复制到原输入数组 */
 59     }
 60 };
 61
 62 int main()
 63 {
 64     vector<int> a = {8,7,6,5,455,88,888,9999,546,46548,1315,445,554,111,5222,2264,8,331,454548};
 65     Solution solution;
 66     solution.InversePairs(a);
 67 return 0;
 68 }