【题解】JSOIWC2019 Round2

题面：

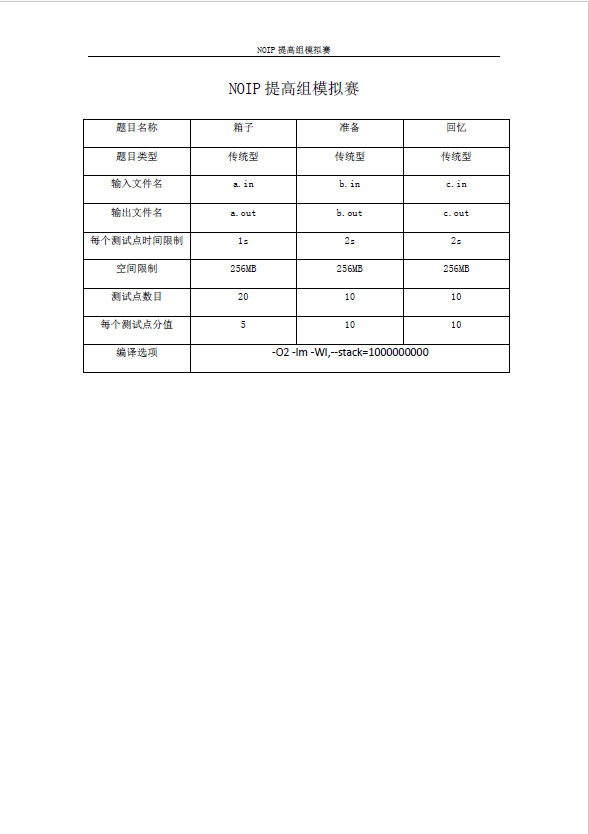
题解：

T1：

毕竟是tg膜你，不会太难

就是一道简单贪心

首先，对于a<=b的所有物品，一定是贪心的按照a从小到大放入。

先假设剩下的物品可以按照某种顺序放进去，那么可以得到一个最终空间（如果最终空间<0那么一定不可行）。

之后可以看成是从结束状态往回还原，还原一个物品需要扣掉b的空间，再加上a的空间，由于b>a所以是一个和前面一样的问题，按照b从小到大排序即可。

#include <bits/stdc++.h>
#define N 100005
#define ll long long
using namespace std;
inline ll read()
{
	register ll x=0,t=1;register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')t=-1;ch=getchar();}
	while('0'<=ch&&ch<='9')x=(x<<3)+(x<<1)+ch-48,ch=getchar();
	return x*t;
}
inline void write(register int x)
{
	if(!x)putchar('0');if(x<0)x=-x,putchar('-');
	static int s[25];register int top=0;
	while(x){s[top++]=x%10,x/=10;}
	while(top)putchar(s[--top]+48);
}
struct node{
	int cost,ret;
}a[N];
inline bool cmp1(register node a,register node b)
{
	return a.cost<b.cost;
}
inline bool cmp2(register node a,register node b)
{
	return a.ret>b.ret;
}
int t,n;
ll v;
inline void lxldl()
{
	n=read(),v=read();
	for(register int i=1;i<=n;++i)
		a[i].cost=read(),a[i].ret=read();
	sort(a+1,a+n+1,cmp1);
	for(register int i=1;i<=n;++i)
		if(a[i].cost<a[i].ret)
		{
			if(a[i].cost>v)
			{
				puts("No");
				return;
			}
			v+=a[i].ret-a[i].cost;
			a[i].ret=a[i].cost=0;
		}
	sort(a+1,a+n+1,cmp2);
	for(register int i=1;i<=n;++i)
		if(a[i].cost<=v)
			v+=a[i].ret-a[i].cost;
		else
		{
			puts("No");
			return;
		}
	puts("Yes");
}
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	t=read();
	while(t--)
		lxldl();
	return 0;
}

T2:

想着各种数据结构，结果是个膜你？

由于是循环位移，所以移动N次之后方案会循环，那么只要考虑前N次移动就可以了。如果把这个绝对值的符号分情况讨论，对于一个数，它在某几次循环位移的时候会使得答案+1，在某几次循环位移的时候会使得答案-1（从1移动到N的情况可以单独考虑），并且+1和-1的时刻分别是一段区间。那么可以维护每次移动后相对于上次的变化量，维护这个变化量的时候需要区间+1/-1，查询每个位置的和。可以使用线段树，但是是在所有操作之后进行询问，所以可以用差分。

#include<bits/stdc++.h>
#define maxn 2000010
#define ll long long
using namespace std;
ll pre[maxn];
int main()
{
	freopen("b.in", "r", stdin);
	freopen("b.out", "w", stdout);
	ll sum = 0, res = 1e18;
	int n;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		int x;
		scanf("%d", &x);
		sum += abs(x - i);
		if (x > i)
		{
			pre[1]++; pre[i]--;
			pre[i] += abs(x - n) - abs(x - 1);
			pre[i + 1] -= abs(x - n) - abs(x - 1);
			int tmp = n - x + i;
			pre[i + 1]--; pre[tmp + 1]++;
			pre[tmp + 1]++; pre[n]--;
		}
		else
		{
			int tmp = i - x;
			pre[1]--; pre[tmp + 1]++;
			pre[tmp + 1]++; pre[i]--;
			pre[i] += abs(x - n) - abs(x - 1);
			pre[i + 1] -= abs(x - n) - abs(x - 1);
			pre[i + 1]--; pre[n]++;
		}
	}
	res = sum;
	for (int i = 1; i <= n - 1; i++)
	{
		pre[i] += pre[i - 1];
		sum += pre[i];
		res = min(res, sum);
	}
	printf("%lld\n", res);
	return 0;
}

T3:

写个打暴力都有70pts，想什么正解（smog

正解也很简单，就是个线段树qaq

分两种情况考虑，先考虑两个线段不相互包含的情况。枚举左端点靠左的那一条线段i，另一条线段j的要求是l[j]在l[i]到r[i]之间，并且产生的答案是(r[j]-l[i])-(r[i]-l[j])，化简一下就是(l[j]+r[j])-([i]+r[i])可以用线段树按照l[j]为关键字维护l[j]+r[j]的最大值。另一种情况就是两条线段包含，依然枚举左端点靠左的那一条线段i，发现另一条线段需要维护r[j]-l[j]的最大值，也是用一棵线段树即可。

···cpp

include <bits/stdc++.h>

define N 200005

using namespace std;

inline int read()

{

register int x=0,t=1;register char ch=getchar();

while(ch<'0'||ch>'9'){if(ch'-')t=-1;ch=getchar();}

while('0'<=ch&&ch<='9')x=(x<<3)+(x<<1)+ch-48,ch=getchar();

return x*t;

}

inline void write(register int x)

{

if(!x)putchar('0');if(x<0)x=-x,putchar('-');

static int s[25];register int top=0;

while(x){s[top++]=x%10,x/=10;}

while(top)putchar(s[--top]+48);

}

inline int Min(register int a,register int b)

{

return a<b?a:b;

}

inline int Max(register int a,register int b)

{

return a>b?a:b;

}

struct node{

int l,r;

}w[N];

inline bool cmp(register node a,register node b)

{

return a.lb.l?a.r>b.r:a.l<b.l;

}

int n,a[N<<1],m=0;

struct SegmentTree{

int minn[N<<4];

inline void init()

{

memset(minn,0x3f,sizeof(minn));

}

inline void pushup(register int x)

{

minn[x]=Min(minn[x<<1],minn[x<<1|1]);

}

inline void update(register int x,register int l,register int r,register int pos,register int v)

{

if(l==r)

{

minn[x]=Min(minn[x],v);

return;

}

int mid=l+r>>1;

if(pos<=mid)

update(x<<1,l,mid,pos,v);

else

update(x<<1|1,mid+1,r,pos,v);

pushup(x);

}

inline int query(register int x,register int l,register int r,register int L,register int R)

{

if(L<=l&&r<=R)

return minn[x];

int mid=l+r>>1;

int res=0x3f3f3f3f;

if(L<=mid)

res=Min(res,query(x<<1,l,mid,L,R));

if(R>mid)

res=Min(res,query(x<<1|1,mid+1,r,L,R));

return res;

}

}tr1,tr2;

int main()

{

freopen("c.in","r",stdin);

freopen("c.out","w",stdout);

n=read();

for(register int i=1;i<=n;++i)

{

w[i].l=read(),w[i].r=read();

a[++m]=w[i].l,a[++m]=w[i].r;

}

sort(w+1,w+n+1,cmp);

sort(a+1,a+1+m);

m=unique(a+1,a+1+m)-(a+1);

for(register int i=1;i<=n;++i)

{

w[i].l=lower_bound(a+1,a+1+m,w[i].l)-a;

w[i].r=lower_bound(a+1,a+1+m,w[i].r)-a;

}

tr1.init(),tr2.init();

int ans=0;

int x;

for(register int i=1;i<=n;++i)

{

x=tr1.query(1,1,m,w[i].r,m);

ans=Max(a[w[i].l]-a[w[i].r]-x,ans);

x=tr2.query(1,1,m,w[i].l,w[i].r);

ans=Max(a[w[i].l]+a[w[i].r]-x,ans);

tr1.update(1,1,m,w[i].r,a[w[i].l]-a[w[i].r]);

tr2.update(1,1,m,w[i].r,a[w[i].l]+a[w[i].r]);

}

write(ans);

puts("");

return 0;

}

#### 这场比赛很简单

#### 暴力分给的很足，

#### 本能能ak的，最后我只有大众分100+50（BIT写挂）+70（暴力+剪枝）=220pts

#### gsy他235，cyc好像245

#### 深深的感受到自己的弱小~