2017.08.06【NOIP提高组】模拟赛B组

Summary

　　今天的比赛60+100+100=260分，没有想到第一题正解是搜索，我与AK差一段距离，这段距离，叫倒着搜。总的来说不是很难。

Problem

T1 天平

题目大意

　　给你N个排序好的砝码的质量，从第三个砝码开始，它的重量最少是前两个砝码的质量之和。天平容不得超过C质量的质量。问最大的质量可以是多少。

想法

　　一般Usaco的题目都不会水到哪里去，但是今天的。。。

　　有两种方法。

（1） 爆搜+剪枝

　　爆搜应该都会，参数是枚举到第K个，当前砝码是重S

　　优化一：如果当前的砝码质量加上没有抉择（没有递归到）的砝码质量还是不能比当前得出的最大值大，则剪枝

　　优化二：倒着搜可以减少之后的分支，当然可以降低时间复杂度，是个很了得的东西，有道题靶形数独同样适用这种方法。

（2） 中途相遇法

　　这个方法效率很玄，但是总比爆搜稳妥

　　可以把1~(n+1)/2和(n+1)/2~n这两段的方案数用dfs求出来，然后枚举。

　　可以用二分来找，最好用两个指针。

T2 游历的路线 

题目大意

　　在从1城市开开始走到n城市，期间有m天，其中第m天一定要在n城市，两两城市之间来或往的马车费用是周期性的，并且有些时候可能不可以从某个城市去另一个城市，问满足条件的最小费用。

想法

　　显然可以用动态规划。

　　设f[i,j]表示第i天到第j城市

　　显然需要知道i-1天在哪个城市，我们可以枚举，设i-1天在k城市

　　f[i,j]=min{f[i-1,k]+s}（其中s代表费用，费用的周期可以用除法原理来算(x-1) mod y+1）

　　初始化显然，效率显然，答案显然。

T3 最短路（shortest）

题目大意

　　求从(0,0)~(n,m)经过点的和的最小值。

　　第(x,y)点的权值为f[x,y]，他的计算方法是f[x,y]=f[x-1,y]+f[x,y-1]，如果(x=0) or (y=0)那么f[x,y]的值为1

想法

　　通过一系列的对拍，我们可以发现，如下图红边的走法，必定最优，但不知道怎么证明。我们设较短边的长为n，较长边的长为m

　　

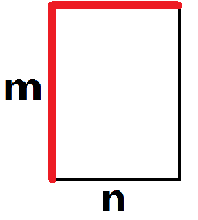
　　我们可以总结成一个公式

　　

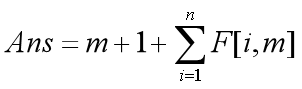
　　那么，关键就成了如何求出F[i,m] (i=1~n)。

　　我们考虑把他转化成组合数的形式

　　根据题目给出的F数组计算方法，可以得出f[x,y]=C(min(x,y),x+y)

　　那么显然F[i,m] (i=1~n)就是C(i,i+m) (i=1~n)

　　其实每个组合数，可以理解成一个数除另一个数，比如对于C(n,m)

　　

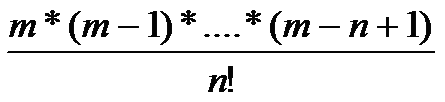
　　试想一下，如果x<y，求C(x,y)+C(x+1,y+1)+C(x+2,y+2)，我们设上面这个式子分子为tot1，分母为tot2

　　C(x+1,y+1)相比C(x,y)的tot1和tot2，发现tot1多乘了y+1，tot2多乘了x+1，

　　C(x+2,y+2)相比C(x+1,y+1)的tot1和tot2，发现tot1多乘了y+2，tot2多乘了x+2

　　说明，我们每次循环，tot1都乘i+m，tot2都乘i，那么，每次的C(i,i+m)就是tot1/tot2

　　但是问题来了,tot1和tot2都很大，如果相除是不太可能的，先mod再除答案是错误的，只能使用逆元了。

逆元

　　根据费马小定理可以得到如下式子

　　

　　两边同时除b得到，高斯研究过，发现是等价的

　　

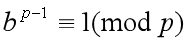
　　 两边同时除b得到，高斯研究过，发现是等价的

　　

　　两边同时乘一个a，并且交换位置，得到如下式子

　　

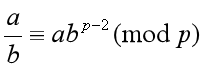
　　 发现，我们要求a除b取模p的结果，其实是等价于ab^p-2取模p的结果的，也就是说，欲想知道a除b取模p的结果，其实就是算出ab^p-2取模p的结果就行了

　　因为a*b mod p，是等价于a mod p*b mod p的，a^k mod p是等价于(a mod p)^k的，所以我们这里可以取mod来避免高精度。

　　当然，F[i,m] (i=1~n)这一部分，可以使用一个组合公式就可以了，具体实现和题解请选手自行考虑。