【APIO2016】烟火表演

题面

题解

神仙题目啊QwQ

设\(f_i(x)\)表示以第\(i\)个点为根的子树需要\(x\)秒引爆的代价。

我们发现，这个函数是一个下凸的一次分段函数。

考虑这个函数合并到父亲节点时会发生怎样的变化。

设\(f_i'(x)\)是原函数，\(f_i(x)\)是新函数，\(i\)和父亲之间的边长度为\(l\)，\([L, R]\)是\(f_i'(x)\)斜率为\(0\)的那一段的左右端点的横坐标，那么有：

\[f_i(x) =
\begin{cases}
f_i'(x) + l & x \leq L \\
f_i'(L) + (l - (x - L)) & L < x \leq L + l \\
f_i'(L) & L + l < x \leq R + l \\
f_i'(L) + ((x - R) - l) & R + l < x
\end{cases}
\]

我们一个一个来看。

首先第一个，当\(x \leq L\)时，我们肯定要让新的\(l\)越小越好，因为改变\(l\)的代价为\(1\)，而这个函数在\(\leq L\)的时候斜率\(\leq -1\)，即修改一次\(x\)的代价\(\geq 1\)，所以干脆将\(l\)变成\(0\)。

第二个，我们只要保证\(x = L\)就能取到函数的最小值，于是\(l\)的变化量越小越好。

第三个，我们不用改变\(l\)就可以保证能取到最小值，那就不用改变了。

第四个和第一个很像，这里就略去了。

---

那么这个过程究竟对这个函数做了什么改变呢？

我们将\(\leq L\)部分的函数向上平移了\(l\)单位，将\([L,R]\)部分向右平移\(l\)单位，在\([L,L+l]\)部分插入了一条斜率为\(-1\)的直线，并将\(> R + l\)的部分的斜率改为了\(1\)。

于是大概变成了这个样子（图源网络）：

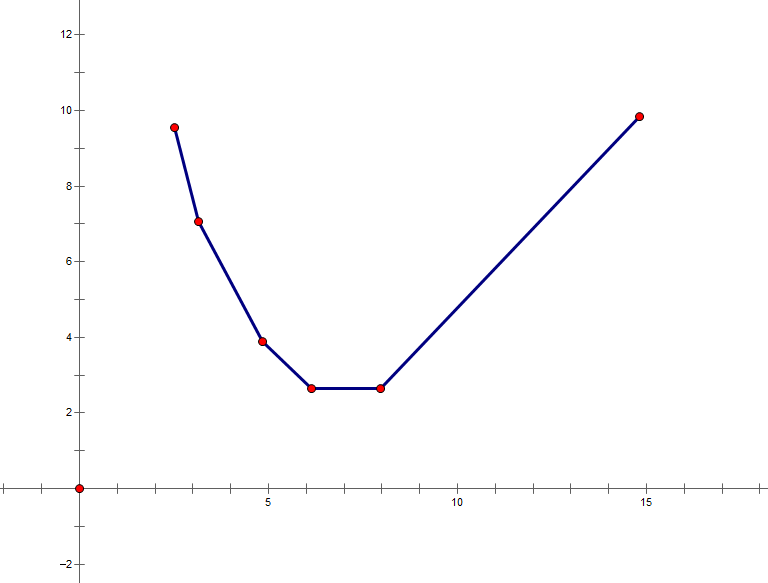
这样，各个拐点之间的直线的斜率是从左到右递增的。

我们不妨假设各个拐点之间的直线斜率的增量为\(1\)，如果有一个斜率不存在，那么我们就用两个同一位置的拐点来表示这个不存在的斜率。

然后我们发现我们只可能存下拐点的横坐标，于是怎么求函数值是一个问题。

我们如果能知道\(f(0)\)的值，这个事情就好办了。

\(f(0)\)的值还不好求？？？就是所有边权之和啊。

于是我们得到了通过拐点横坐标求得\(f(L)\)的方法，皆大欢喜。

那么我们知道每个函数被合并上去之前会变成什么样子了，那么我们也可以非常简单的合并两个函数了，我们只需要将两个函数的拐点列表合并一下就可以了。

我们再看看在合并到父亲节点时要做的操作：

一、将斜率\(> 0\)的那一段的斜率改为\(1\)。

因为我们合并上来的函数的斜率最大值都为\(1\)，所以我们只需要删除\(k - 1\)个最大的拐点即可，其中\(k\)是这个点儿子的数量。

二、将斜率\(=0\)的那一段平移\(l\)单位。

首先，我们做完一操作之后，横坐标最大的两个拐点就是斜率为\(0\)的两个端点了，将它们弹出来，加上\(l\)再放进去就没了。

三、加入一段斜率为\(-1\)的直线。

这个其实在做操作二的时候就顺带做完了。

我们维护一个可并堆就可以做上面的所有操作。

最后求答案时，我们保留\(L\)及其左边的拐点，依次减去它们的横坐标就是我们想要的函数值了。

代码

代码倒是比想象中的要短。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define RG register
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)

namespace IO
{
	const int BUFSIZE = 1 << 20;
	char ibuf[BUFSIZE], *is = ibuf, *it = ibuf;
	inline char getchar() { if (is == it) it = (is = ibuf) + fread(ibuf, 1, BUFSIZE, stdin); return *is++; }
}

inline int read()
{
	int data = 0, w = 1;
	char ch = IO::getchar();
	while(ch != '-' && (ch < '0' || ch > '9')) ch = IO::getchar();
	if(ch == '-') w = -1, ch = IO::getchar();
	while(ch >= '0' && ch <= '9') data = data * 10 + (ch ^ 48), ch = IO::getchar();
	return data * w;
}

const int maxn(600010);
int n, m, cur, fa[maxn], C[maxn], deg[maxn], rt[maxn];
struct node { int lson, rson, dis; long long x; } t[maxn];
long long ans;

int merge(int x, int y)
{
	if(!x || !y) return x | y;
	if(t[x].x < t[y].x) std::swap(x, y);
	t[x].rson = merge(t[x].rson, y);
	if(t[t[x].lson].dis < t[t[x].rson].dis) std::swap(t[x].lson, t[x].rson);
	if(!t[x].rson) t[x].dis = 0; else t[x].dis = t[t[x].rson].dis + 1;
	return x;
}

inline int pop(int x) { return merge(t[x].lson, t[x].rson); }
int main()
{
#ifndef ONLINE_JUDGE
	file(cpp);
#endif
	n = read(), m = read();
	for(RG int i = 2; i <= n + m; i++)
		++deg[fa[i] = read()], ans += (C[i] = read());
	for(RG int i = n + m; i > 1; i--)
	{
		long long l = 0, r = 0;
		if(i <= n)
		{
			while(--deg[i]) rt[i] = pop(rt[i]);
			r = t[rt[i]].x, rt[i] = pop(rt[i]);
			l = t[rt[i]].x, rt[i] = pop(rt[i]);
		}
		t[++cur].x = l + C[i], t[++cur].x = r + C[i];
		rt[i] = merge(rt[i], merge(cur, cur - 1));
		rt[fa[i]] = merge(rt[fa[i]], rt[i]);
	}
	while(deg[1]--) rt[1] = pop(rt[1]);
	while(rt[1]) ans -= t[rt[1]].x, rt[1] = pop(rt[1]);
	printf("%lld\n", ans);
	return 0;
}