培训补坑(day8:树上倍增+树链剖分)

补坑补坑。。

其实挺不理解孙爷为什么把这两个东西放在一起讲。。当时我学这一块数据结构都学了一周左右吧（超虚的）

也许孙爷以为我们是省队集训班。。。

好吧，虽然如此，我还是会认真写博客（保证初学者不会出现看不懂的情况啦，如果有的话可以在博客下方留言QAQ，我会尽量解答的。。）

首先先讲一下倍增：

倍增的思想是这样的：

比如我们知道a[1]->a[2],a[2]->a[3],a[3]->a[4]这样的关系

那么我们如果按照普通的方法通过a[1]->a[4]的话，那么我们要将所有的情况遍历一遍。

但是如果我们预处理出倍增数组f[i][j]表示a[i]往后推2^j次后得到的结果，那么我们就能用logn解决这个问题。

下面展示一下预处理过程:

f[1][0]=2;f[2][0]=3;f[3][0]=4

f[1][1]=3;f[2][1]=4;

所以我们先找到f[1][1],再找到f[3][0]就可以找到a[4]了（是不是很神奇）

那么我们既然在线性上可以倍增，那么在树上是否也可以倍增呢？答案是：可以。

所以我们最典型的树上倍增问题就是求LCA。

那么我们怎么求LCA呢？

下面上图：

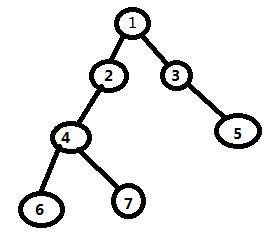
在这个图中，我们要求6与5的最近公共祖先。

而对于倍增算法来说，求LCA有两个步骤：

1、让两个点的深度相同（如果找到公共祖先就直接输出）

2、让两个点同时向上走同样的步数。

我们先用倍增让6号点走到和5号点的深度相同的4号点。

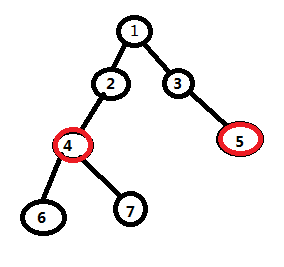
接下来我们试着让这两个点同时向上走2^i,2^i-1...2^0步，如果我们发现他们不是同一个点，那么就往上走。不然就不走。

这样就会到达2和3号点

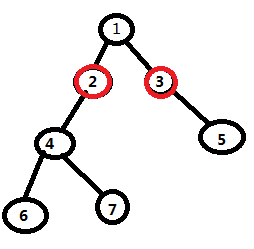
在这之后，我们就会发现，两个点再往下走一步就是他们的LCA啦！

这就是倍增求LCA的方法

下面附上求LCA的代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct data{
    int next,to;
}g[];
int depth[];
int que[];
bool visit[];
int head[];
int fa[][];
int n,q,root,num=;
int lca(int u,int v){
    if(depth[u]<depth[v])swap(u,v);
    int dc=depth[u]-depth[v];
    for(int i=;i<=;i++)
    if((<<i)&dc&&fa[i][u]){
    u=fa[i][u];
    }
    if(u==v)return u;
    for(int i=;i>=;i--)
    if(fa[i][u]!=fa[i][v]&&fa[i][u]){
    u=fa[i][u];
    v=fa[i][v];
    }
    return fa[][u];
}
void bfs(int u)
{
    memset(que,,sizeof(que));
    memset(visit,,sizeof(visit));
    visit[u]=true;
    que[]=u;
    int h=,l=;
    while(h<=l)
    {
        int rt=que[h];
        for (int i=head[rt];i;i=g[i].next)
        {
            int v=g[i].to;
            if ( !visit[v] )
             {
                    visit[v]=true;
                    depth[v]=depth[rt]+;
                    que[++l]=v;
             }
        }
        h++;
    }
}
int main(){
    scanf("%d%d",&n,&q);
    memset(g,,sizeof(g));
    memset(fa,,sizeof(fa));
    memset(depth,,sizeof(depth));
    for(int i=;i<n;i++)
    {
    int f,t;
    scanf("%d%d",&f,&t);
    g[++num].next=head[f];
    head[f]=num;
    g[num].to=t;
    fa[][t]=f;
    if(fa[][f]==)root=f;
    }
    for(int j=;j<=;j++)
    for(int i=;i<=n;i++)
    {

        fa[j][i]=fa[j-][fa[j-][i]];
    }
    depth[root]=;
    bfs(root);
    for(int i=;i<=q;i++){
    {
        int num1,num2;
        scanf("%d%d",&num1,&num2);
        printf("%d\n",lca(num1,num2));
    }
    }
}

——————————————————我是分割线——————————————————

讲完了树上倍增，我们来到这节课的重点：树链剖分

树链剖分简单来说，就是把一颗树切成许多的链，使原来的对点的访问变成对一条链的访问来加速算法，所以树链剖分是用来处理树上区间问题的。

那么我们首先要引入一个概念：重链。

重链，顾名思义（它比较重，，） ，它指的是一条链上的点都是重儿子。。。

之所以叫做重儿子，是因为它的子树的节点数大于其他儿子的子树的节点数。

比如在这个图中，红色的点就是蓝色点的重儿子：

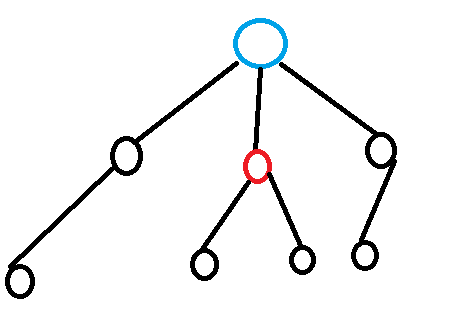
那么对于其他的儿子，他们也会组成由它们自己为链头的重链。所以我们就把整棵树变成了一条条链。

那么这到底有什么优化呢？因为一个理论：从根节点到树上的任意一个点最多只会经过logn条重链。所以我们可以保证每次查询复杂度为O(logn)

这就是优化的方法。

那么我们懂得了如何剖分之后，我们来想想如何查找。

就拿最经典的问题来说：LCA

那么我们知道，假设我们把2个点都往上爬，当他们爬到了同一条链上的时候，我们就不用继续往上爬了，因为我们知道他们的LCA就是这2个点中深度较浅的一个点。

然后显然我们要让两个点的深度之差变得更小，而不是让它变得更大，所以当我们发现两个点不在同一条链上的时候，我们就让深度较深的这个点爬到它所在的链的顶端的父节点。

然后当他们在同一条链上的时候直接输出较浅的点即可。

具体代码实现如下：

int lca(int x,int y)
{
    while(top[x]!=top[y])
        if(dep[top[x]]>dep[top[y]])x=fa[top[x]];
        else y=fa[top[y]];
    return dep[x]<dep[y]?x:y;
} 

那么有时候我们是要在树上的一段区间进行修改，那么显然我们不能这么简单的修改，因为我们区间修改的操作一般是在线段树上进行的，如果我们不能知道这个点在线段树上的什么位置，那么我们就无法进行修改

而对于这个问题，我们引进一个pos数组，表示的是这个点第一次在dfs序中出现的位置，这样我们每次在pos[top[x]],pos[x]这一段修改就好啦。具体实现如下。（这里贴的是区间查询的代码。区间修改的改一改就好了QAQ）

long long mquery(int x){
    register long long res=;
    while(top[x]!=)res+=query(,n,pos[top[x]],pos[x],),x=fa[top[x]];
    return res+=query(,n,pos[],pos[x],);
}

希望大家能够看懂。。看不懂真的抱歉，可能是我比较弱，说不清楚，所以有问题都可以问我啦：QQ：471751802

还有，后面我会把所有树剖的题目都贴到博客上，有空的小伙伴们可以去看看咯