BFS和图的最短路径 279，127，126

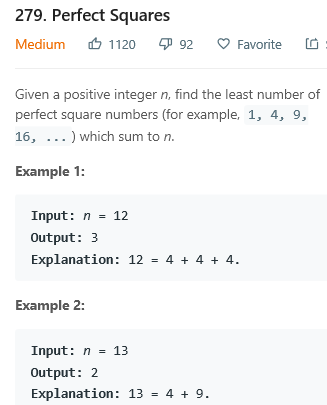
在本题中，任何一个正整数都会由完全平方数1组成，所以不可能没有解。

贪心是不成立的，因为如果寻找12的完全平方数，使用贪心，则它由9，1，1，1四个数组成；但是最少的完全平方数是由三个4组成的。

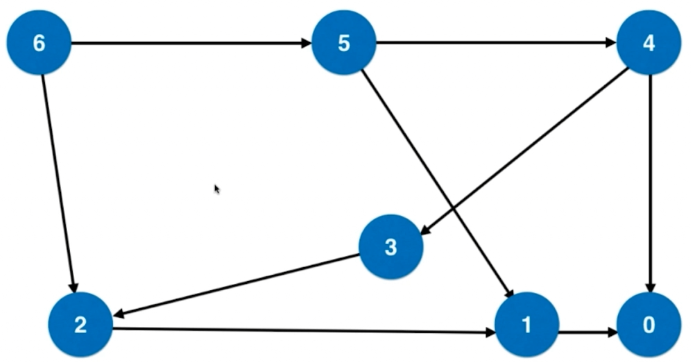
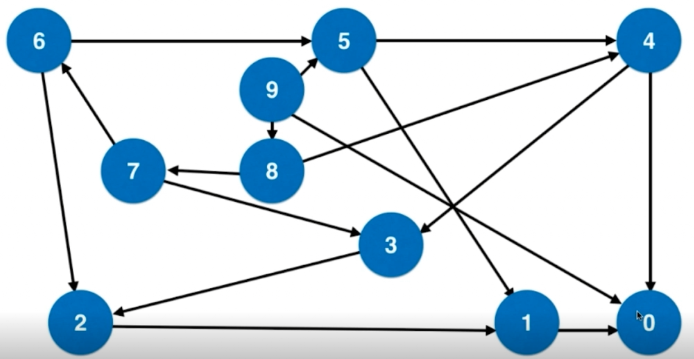
4->3->2->1->0 之间相差1，这个完全平方数；

4->0 之间相差4，这个完全平方数。

class Solution {
public:
    int numSquares(int n) {
        //图的广度优先遍历
        queue< pair<int, int> > q;    //具体第几个数字；图中经历了几段路径到达这个数字
        q.push(make_pair(n,));    //对于n这个数字，0步到达

        vector<bool> visited(n+, false);   //0 - n 这n+1个结点有没有被访问过
        visited[n] = true;    //n一开始已经被推入栈中了

        while(!q.empty()){
            //取出队首元素
            int num = q.front().first;  //这个数字是多少
            int step = q.front().second;   //走了几步
            q.pop();

            for(int i=; ; i++){
                int a = num-i*i;
                if(a<)
                    break;
                if(a == )
                    return step+;
                if(!visited[a]){    //当visited这个结点没有被访问过时，将它推入，避免重复计算
                    //说明除了i之外还能有一个完全平方数
                    q.push(make_pair(a, step+));
                    visited[a] = true;
                    }
                }
        }
        throw invalid_argument("No Solution.");
    }
};

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        unordered_set<string> wordSet(wordList.begin(), wordList.end());

        if(!wordSet.count(endWord))    //若给定单词列表没有endWord，返回
            return ;

        queue<pair<string, int>> q;
        q.push(make_pair(beginWord, ));

        while(!q.empty()){
            string word = q.front().first;
            int res = q.front().second;
            q.pop();

            if(word == endWord)
                return res;

            for(int i=;i<word.size();i++){
                string newWord = word;
                for(char ch='a'; ch<='z';ch++){
                    newWord[i] = ch;
                    if(wordSet.count(newWord) && newWord!=word){
                        q.push(make_pair(newWord, res+));
                        wordSet.erase(newWord);
                    }
                }
            }
         }
        return ;
    }
};

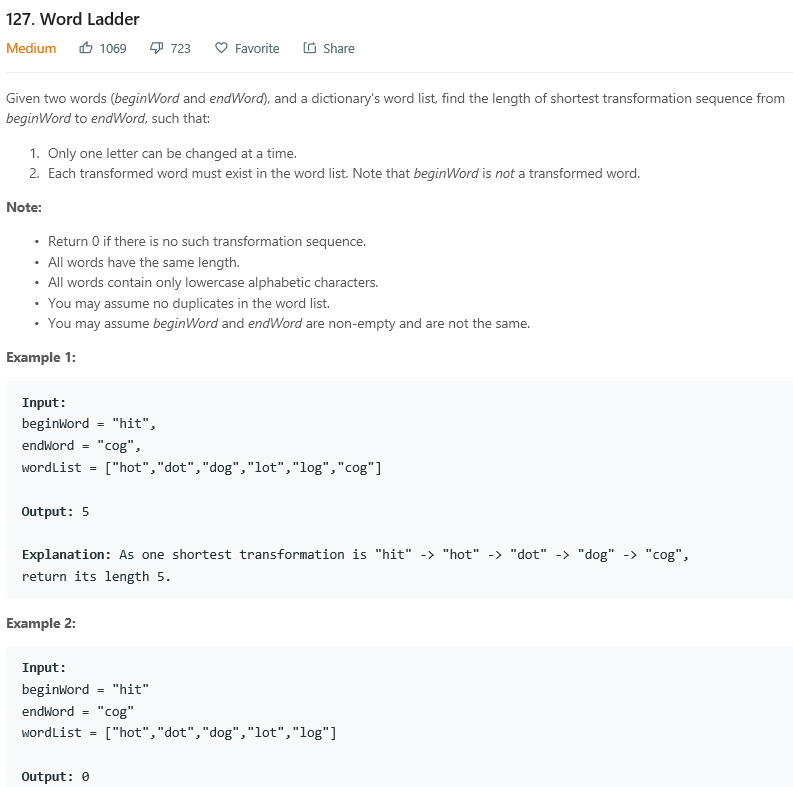
127这道题需要注意的是：如果不把vector里存储的数据用set来存，就会导致 time limited 的问题！！

class Solution {
public:
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {

        vector<vector<string>> res;   //res保存最短路径

        unordered_set<string> dict(wordList.begin(), wordList.end());   //dict保存单词列表

        queue<vector<string>> paths;  //保存所有可能路径
        paths.push({beginWord});

        int level = , minLevel = INT_MAX;     //level存储当前路径，minLevel最短路径

        unordered_set<string> words;    //存储已经遍历过的单词

        while(!paths.empty()){

            vector<string> t = paths.front();   //队列中首路径
            paths.pop();

            if(t.size()>level){
                //把已经遍历过的单词在dict中删除
                for(string a:words) dict.erase(a);
                words.clear();  //words清零 准备储存下一次遍历的单词
                level = t.size();

                //剪枝
                if(level > minLevel)
                    break;

            }

            string last = t.back();   //last存储当前路径的最后一个单词
            for(int i=; i<last.size();i++){
                string newlast = last;
                for(char ch ='a';ch<='z';ch++){
                    newlast[i] = ch;
                    if(!dict.count(newlast))
                        continue;   //若dict中找不到这个单词，退出本次循环
                    words.insert(newlast);    //插入到已遍历列表
                    vector<string> nextPath = t;
                    nextPath.push_back(newlast);

                    if(newlast == endWord){
                        //先找到endWord的路径一定是最短的
                        res.push_back(nextPath);
                        minLevel = level;
                    }
                    else
                        paths.push(nextPath);

                }
            }
        }

        return res;
    }
};

·