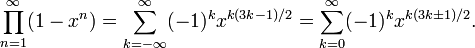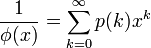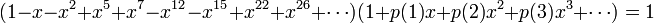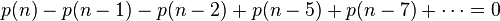hdu 4651 Partition (利用五边形定理求解切割数)
下面内容摘自维基百科:
五边形数定理[编辑]
五边形数定理是一个由欧拉发现的数学定理,描写叙述欧拉函数展开式的特性[1] [2]。欧拉函数的展开式例如以下:
亦即
欧拉函数展开后,有些次方项被消去,仅仅留下次方项为1, 2, 5, 7, 12, ...的项次,留下来的次方恰为广义五边形数。
当中符号为- - + + - - + + .....
若将上式视为幂级数,其收敛半径为1,只是若仅仅是当作形式幂级数(formal
power series)来考虑,就不会考虑其收敛半径。
和切割函数的关系
当中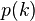 为k的切割函数。
为k的切割函数。
上式配合五边形数定理,能够得到
考虑 项的系数,在
项的系数,在
n>0 时,等式右側的系数均为0,比較等式二側的系数,可得
因此可得到切割函数p(n)的递归式
以n=10为例
-
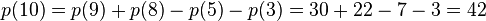
- 知道这个定理的话,hdu 4651就能够直接套模板了
-
#include<algorithm>
#include<iostream>
#include<cstring>
#include<vector>
#include<cstdio>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define MP make_pair
#define LL long long
#define CLR(a, b) memset(a, b, sizeof(a)) using namespace std; const int maxn = 100100;
const int INF = 0x3f3f3f3f;
const LL MOD = 1000000007; int fiv[maxn];
LL p[maxn]; void init()
{
int tot = 1;
for(int i = 1; fiv[tot - 1] < maxn; i ++)///五边形数
{
fiv[tot ++] = i*(3*i-1)/2;
fiv[tot ++] = i*(3*i+1)/2;
}
p[0] = 1;
for(int i = 1; i < maxn; i ++)///i的切割数p(i)
{
p[i] = 0;int flag = 1;
for(int j = 1; ; j ++)
{
if(fiv[j] <= i)
{
p[i] += flag * p[i - fiv[j]];
p[i] = (p[i] % MOD + MOD) % MOD;
}
else break;
if(j % 2 == 0) flag = -flag;
}
}
} int main()
{
int T, n;
init();
scanf("%d", &T);
while(T --)
{
scanf("%d", &n);
printf("%lld\n", p[n]);
}
}
hdu 4651 Partition (利用五边形定理求解切割数)的更多相关文章
- hdu 4651 Partition(整数拆分+五边形数)
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total ...
- hdu - 4651 - Partition
题意:把一个整数N(1 <= N <= 100000)拆分不超过N的正整数相加,有多少种拆法. 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid ...
- hdu 4651 Partition && hdu 4658 Integer Partition——拆分数与五边形定理
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4651 参考:https://blog.csdn.net/u013007900/article/detail ...
- hdu 4651 - Partition(五边形数定理)
定理详见维基百科....http://zh.wikipedia.org/wiki/%E4%BA%94%E9%82%8A%E5%BD%A2%E6%95%B8%E5%AE%9A%E7%90%86 代码如下 ...
- HDU 4651 Partition(整数拆分)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4651 题意:给出n.求其整数拆分的方案数. i64 f[N]; void init(){ f[0 ...
- HDU 4651 Partition 整数划分,可重复情况
Partition Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total S ...
- HDU 4651 (生成函数)
HDU 4651 Partition Problem : n的整数划分方案数.(n <= 100008) Solution : 参考资料: 五角数 欧拉函数 五边形数定理 整数划分 一份详细的题 ...
- 利用JavaScript打印出Fibonacci数(不使用全局变量)
从汤姆大叔的博客里看到了6个基础题目:本篇是第4题 - 利用JavaScript打印出Fibonacci数(不使用全局变量) 解题关键: 1.Fibonacci数列的规律 2.递归 解点1:Fibon ...
- 回数是指从左向右读和从右向左读都是一样的数,例如 12321 , 909 。请利用 filter() 滤掉非回数
不管在什么地方,什么时候,学习是快速提升自己的能力的一种体现!!!!!!!!!!! 最近一段时间学习了廖雪峰老师学的Python学习资料,给自己的帮助很大,同时也学到的了很多,今天做了一道练习题,对于 ...
随机推荐
- 转:在Eclipse中进行C/C++开发的配置方法(20140721最新版)
http://blog.csdn.net/baimafujinji/article/details/38026421 Eclipse 是一个开放源代码的.基于Java的可扩展开发平台.就其本身而言,它 ...
- Android 基础知识点(持续更新)
一.AndroidManifest 每一个安卓工程都有AndroidManifest.xml的配置文件,在所有项目中该名称都不会变.该文件是Android工程的一个全局配置文件,所有在Android中 ...
- Android Canvas使用drawBitmap绘制图片
1.基本的绘制图片方法 //Bitmap:图片对象,left:偏移左边的位置,top: 偏移顶部的位置 drawBitmap(Bitmap bitmap, float left, float top, ...
- How to: Use a Custom User Name and Password Validator
在wcf中使用自定义的用户名和密码验证方式 https://msdn.microsoft.com/en-us/library/aa702565.aspx http://www.codeproject. ...
- 1px
Retina屏的移动设备如何实现真正1px的线? <!DOCTYPE html> <html> <head> <meta charset="utf- ...
- sql server 2005+ 行转列
)) , 'aa') , 'bb') , 'aaa') , 'bbb') , 'ccc') go , , '') from tb group by id
- SharePoint2010沙盒解决方案基础开发——关于TreeView树形控件读取列表数据(树形导航)的webpart开发及问题
转:http://blog.csdn.net/miragesky2049/article/details/7204882 SharePoint2010沙盒解决方案基础开发--关于TreeView树形控 ...
- HDU 5949 Relative atomic mass 【模拟】 (2016ACM/ICPC亚洲区沈阳站)
Relative atomic mass Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Oth ...
- VS发布,TFS邮件设置截图
vs2012发布截图: TFS邮件设置截图:
- [转]NHibernate之旅(7):初探NHibernate中的并发控制
本节内容 什么是并发控制? 悲观并发控制(Pessimistic Concurrency) 乐观并发控制(Optimistic Concurrency) NHibernate支持乐观并发控制 实例分析 ...