关于电脑硬盘的二三事（SATA接口）
@
前言
前一段时间刚装了一台台式机，买的硬盘是m.2的500g固态，但是对于台式机来说的话，还是显得有些小了，所以打算买一个新的扩展盘，过程中也顺带了解了不少知识，由此记录下来也希望给以后买硬盘的朋友做个参考。
接口分类
既然是新增硬盘，那么就要说一说接口了。
大部分主板上都是有一下几种可以接硬盘存储设备的接口，有SATA接口，M.2接口，也有PCI_E接口，我的PCI_E接口上插了网卡，m.2上也已经有一个固态了，多以只能在SATA接口上进行一个加装。这里就基于SATA接口说明。
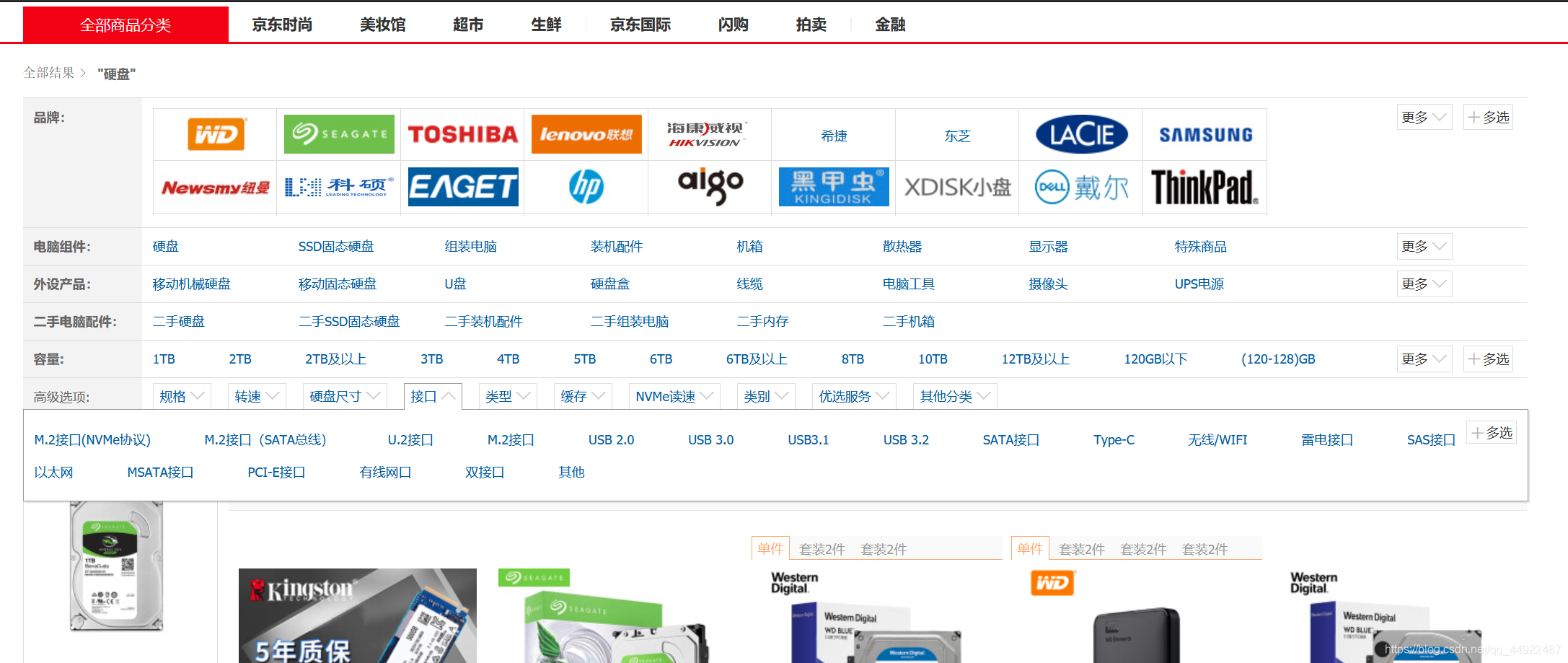在某东搜索硬盘，我们就可以看到有接口分类，而且分类繁多，我这里只说一下我提到的三种接口（因为其他接口我也没去了解过）
SATA3接口
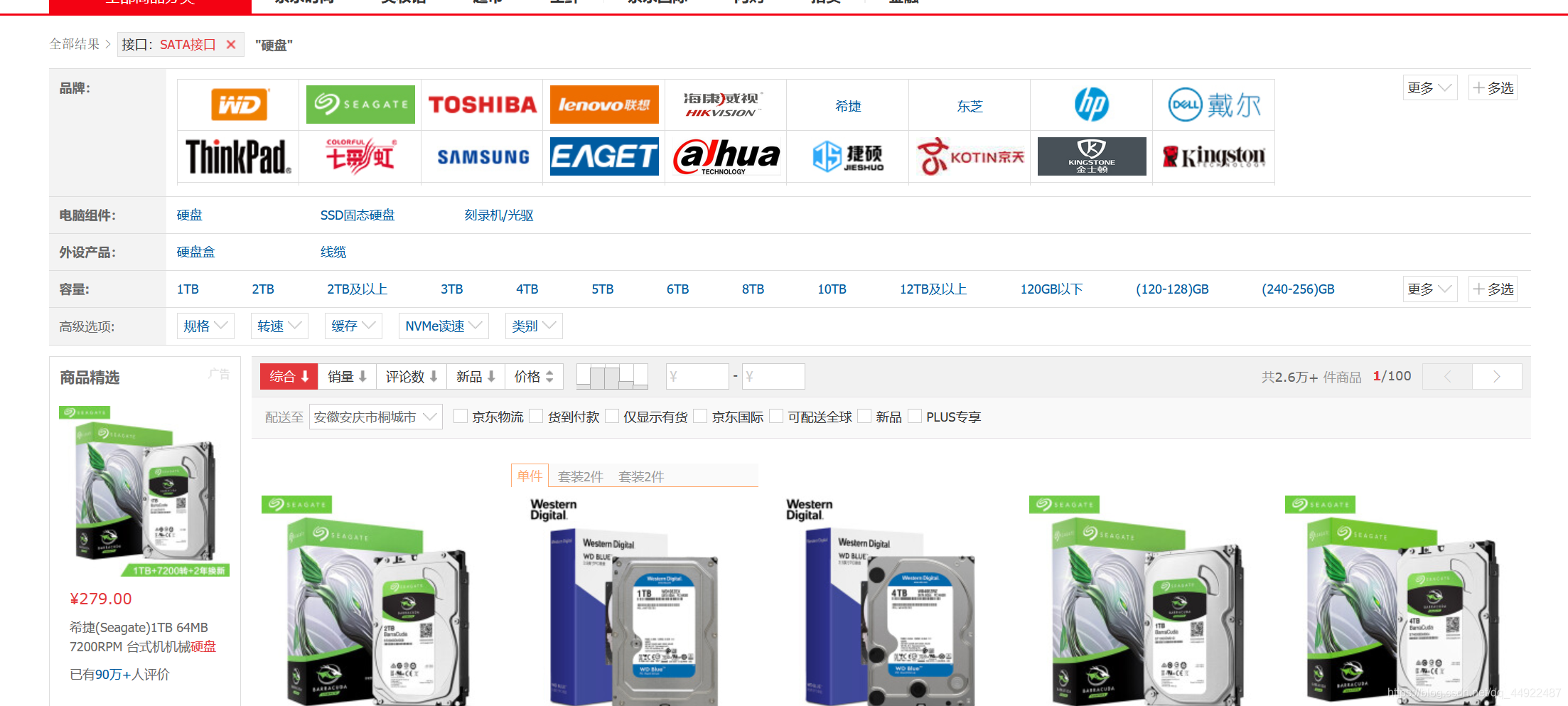
很明显啊，勾选sata接口之后显示的大部分都是机械硬盘，机械硬盘怎么样呢，我可以说说我了解到的：
机械硬盘
机械硬盘的特点和主要参数
机械硬盘最大的特点应该就是便宜容量大还有寿命长了，其他也没什么特点。
这里说主要参数不是全部参数：
读写速度，转速，容量，缓存以及两种不同的方式（垂直式（PMR）和瓦叠式（SMR))
转速现在大多都是7200，机械硬盘嘛，转的越快读得越快（其他变量相同的情况下），同时噪声也有差别，容量就是硬盘大小。 原文:https://www.sohu.com/a/203688929_615464 中午走路的时候,同事说的,M 2 nvme接口的更快. 树莓派开发板可以跑linux . ------------ ... 序 学生时期,有过小组作业,当时分工一人做那么两三个页面,然而在前端差不多的时候,我和另一个同学发生了争执.当时用的是简单的三层架构(DLL.BLL.UI),我个人觉得各写各的吧,到时候合并,而他觉得 ... SATA接口.PCI/PCIe.NVMe的介绍 SATA接口 SATA是Serial ATA的缩写,即串行ATA. SATA已经完全取代旧式PATA(Parallel ATA或旧称IDE)接口的旧式硬 ... LibLinear(SVM包)使用说明之(二)MATLAB接口 LibLinear(SVM包)使用说明之(二)MATLAB接口 zouxy09@qq.com http://blog.csdn.net/ ... Java并发编程二三事 转自我的Github 近日重新翻了一下<Java Concurrency in Practice>故以此文记之. 我觉得Java的并发可以从下面三个点去理解: * ... 匿名内部类适合创建那些只需要使用一次的类,它的语法有些奇怪,创建匿名内部类会立即创建一个该类的实例,这个类定义立即消失,且不能重复使用. 定义匿名类的格式如下: new 实现接口() |父类构造器(实 ... [经验]一只代码小白git托管路上的二三事 写在前面的话 寒假的时候,娄老师给我们布置了代码托管的作业,并要求把托管地址发给学委.因假期的时候没有带电脑回家,所以只是在手机上草草注册了,也稀里糊涂就将 ... 以sata接口(依据linux内核检測其顺序 sda,sdb...)为例, 1, 硬盘的限制,最多仅仅能设置4个分区(主分区+扩展分区),路径例如以下, /dev/sda1 /dev/sda2 ... 关于密码的二三事 关于账号和密码的二三事 久了不更linux的相关知识,实在是懒得想内容点(纯粹是懒).那么今天就来谈谈关于linux密码和账号的重要概念. 假如你的主机遭到入侵,那么对方的第一个侵入 ... 前言 这篇文章会对PHP的MySQL扩展库,MySQLI的扩展库,SQL批量执行,事务控制等等进行一些简单的讲解. MySQL扩展 PHP中MySQL扩展,虽然因为安全的原因,在PHP5.6及往上不在 ... A string s is called an (k,l)-repeat if s is obtained by concatenating k>=1 times some seed strin ... 题意:给定一个队列延迟值为Di的任务,以任意顺序入栈和出栈,第K个出栈的延迟值为(K-1)*Di.问最小的延迟值. 解法:f[i][l]表示完成以第i个任务开始,长度为l,到第i+l-1个任务的最小延 ... console.dir()打印出来的东西不加任何操作 console.log()打印出来东西实现进行了操作,打印出来的东西可能不是原型 具体对象的类型可以在"_proto_"中看, ... 有些情况下,有些脚本命令不能满足我们的需求,而手头却能用C#很方便的实现. 我们就可以把自定义的类型Add到PowerShell中使用,使用方法和PowerShell调用.NET类库方法是一样的. 以 ... 最长异或路径 题目链接:ybt高效进阶2-4-3 / luogu P4551 题目大意 给定一棵 n 个点的带权树,结点下标从 1 开始到 N.寻找树中找两个结点,求最长的异或路径. 异或路径指的是指 ... 前言 受益于pytest的集成,HttpRunner v3.x可以使用pytest所有插件,包括pytest-html和allure-pytest,也可以实现这2种方式的报告 内置html报告 pyt ... 一.获取本机ip 通过ip查询网址来查询本机外网地址 二.下载远程链接软件 下载向日葵,注册账号 三.远程链接 将连接端与被连接端分别绑定账号,输入相应ip地址,即可连接. 目录 删除旧版本 清除未卸载干净的angular-cli缓存 对于Linux 对于Windows 安装最新版本 查看安装版本 创建新项目 删除旧版本 npm uninstall -g angular- ... 工作中遇到需要在windows环境中命令提示符下切换为Guest用户执行程序,类似Linux中的su操作. 操作步骤如下:1.用管理员权限运行cmd.2:执行命令:runas /user:userna ...
买硬盘嘛，最关注的其实还是读写速度。
读写速度这里我这几天逛jd一度被迷惑：
像这种第一眼很容易让小白以为传输速度6G/s,这他妈好6啊，速率6G/s，那盘里的小姐姐不就是来去自如嘛？
关于电脑硬盘的二三事（SATA接口）的更多相关文章
随机推荐