5.15 省选模拟赛 容斥 生成函数 dp

LINK：5.15 T2

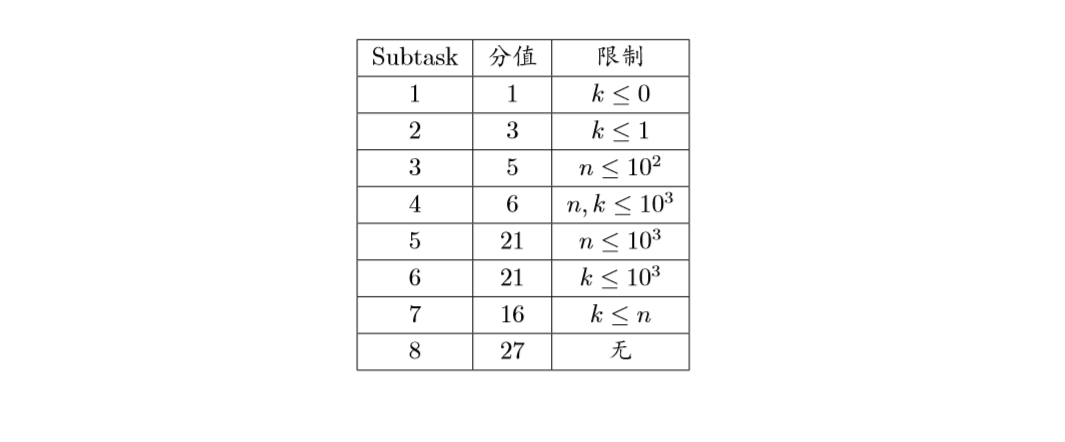
个人感觉生成函数更无脑 容斥也好推的样子.

容易想到每次放数和数字的集合无关 所以得到一个dp f[i][j]表示前i个数字 逆序对为j的方案数.

容易得到转移 使用前缀和优化即可。

进一步的可以设出其生成函数 对于第i次放数字 生成函数为\(F(x)=1+x^1+x^2+...x^{n-i}\)

那么容易得到答案的生成函数为 \(G(x)=\frac{\Pi_{i=1}^{n}(1-x^i)}{(1-x)^n}\)

化简一下 然后dp出来方案数即可 可以发现这个dp是\(k\sqrt n\)

当然也可以容斥 可以发现 其实每个数字都有范围[0,i-1]

我们想要求出 \(g_1+g_2+...g_n=k\)这个等式的解的个数。

此时隔板法可以求出 方程的解 不过不一定满足 范围。

考虑 容斥 总方案-一个不合法+两个不合法-三个不合法...

容易想到 第i个数字不合法当且仅当其值>=i时不合法 那么利用代表元 就很容易统计其不合法方案.

这样问题变成了 求出 f[i][j]表示i个数字和为j的方案数.

显然这i个数字每个都不相同 那么第一维是一个根号的状态.

所以 转移也很简单 不过值得注意的是需要减掉某个数字>n的方案.

这个在第一次越过的时候减掉即可。

两种方案 殊途同归 写法一模一样.

const ll MAXN=100010;
ll n,k,maxx;
ll f[600][MAXN];
ll fac[MAXN<<1],inv[MAXN<<1];
inline ll ksm(ll b,ll p)
{
	ll cnt=1;
	while(p)
	{
		if(p&1)cnt=cnt*b%mod;
		b=b*b%mod;p=p>>1;
	}
	return cnt;
}
inline void prepare()
{
	fac[0]=1;
	rep(1,maxx,i)fac[i]=fac[i-1]*i%mod;
	inv[maxx]=ksm(fac[maxx],mod-2);
	fep(maxx-1,0,i)inv[i]=inv[i+1]*(i+1)%mod;
}
inline ll C(ll a,ll b){return a<b?0:fac[a]*inv[b]%mod*inv[a-b]%mod;}
signed main()
{
	freopen("b.in","r",stdin);
        freopen("b.out","w",stdout);
	get(n);get(k);
	maxx=n+k;prepare();
	ll ww=(ll)sqrt(k*2*1.0)+1;
	f[0][0]=1;
	rep(1,ww,i)
	{
		rep(1,k,j)
		{
			if(j>=i)f[i][j]=(f[i][j-i]+f[i-1][j-i])%mod;
			if(j>n)f[i][j]=(f[i][j]-f[i-1][j-n-1])%mod;
		}
	}
	ll ans=0;
	rep(0,ww,i)
	{
		rep(0,k,j)
		{
			if(i&1)ans=(ans-f[i][j]*C(k-j+n-1,n-1))%mod;
			else ans=(ans+f[i][j]*C(k-j+n-1,n-1))%mod;
		}
	}
	putl(M(ans));
	return 0;
}