OpenCV 之 支持向量机 (一)

机器学习是由 模型 + 策略 + 算法 构成的，构建一种机器学习方法 (例如，支持向量机)，就是具体去确定这三个要素。

1  支持向量机

支持向量机，简称 SVM (Support Vector Machine)，是一种二分分类模型。

1) 模型 (model)

定义在特征空间上的，一种间隔 (margin) 最大的，线性分类器 (linear classifier)

2) 策略 (strategy)

使间隔最大化，可转化为求解凸二次规划的问题。

3) 算法 (algorithm)

求解凸二次规划的最优化算法。

供训练的样本数据可分为三类：第一类是线性可分的，第二类是近似线性可分的，第三类是线性不可分的。

三种样本数据对应的 SVM 分别为：线性可分 (硬间隔最大化)，线性 (软间隔最大化)，非线性 (核技巧 + 软间隔最大化)。

为了方便起见，下文提到的向量机 或 SVM，都是指线性可分支持向量机。

2  基本概念

2.1  超平面 (hyperplane)

n 维欧式空间中，余维度等于 1 (也即 n-1 维) 的线性子空间，称为超平面。

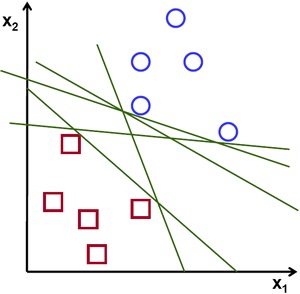
超平面在二维空间中是直线，在三维空间中是平面，可用来分隔数据。如下图所示，超平面 (直线) 能将两类不同的数据 (圆点和方点) 分隔开来。

如果将数据点记为 x (n 维向量)，则超平面的方程为 $\ f(x) = \beta_{0} + \beta^{T} x = 0\; $，其中，$\beta $ 为权重向量 (有的书称为 “法向量”)

             

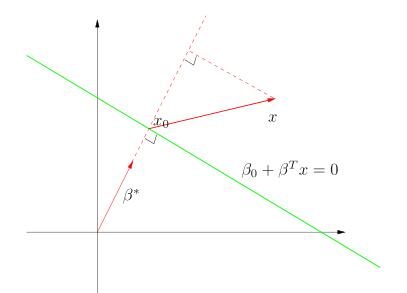
解释：右图中 $\beta^{*}$ 为超平面 (绿色直线) 的单位法向量 $\ \beta^{*} = \dfrac{\beta}{||\beta||}$，平面中任意点 x 到超平面的距离为 $\ r = \dfrac{|\beta_{0} + \beta^{T} x|} {||\beta||}$

又附： 平面坐标中，一个点 $\;(x_{0}, y_{0})\;$到直线$\;(Ax + By + C = 0)\;$ 的距离为 $\; d = \dfrac{Ax_{0} + By_{0} + C}{\sqrt{A^{2} + B^{2}}} $

2.2  支持向量 (support vector)

如果取输出 y 分别为 +1 和 -1，代表两种不同类别，则对于 x，其对应的 f(x) 有三种可能取值：

1) 当位于超平面上时 (也即图中的直线上)，$ f(x) = \beta_{0} + \beta^{T} x = 0 $

2) 当位于超平面左边时， $f(x) = \beta_{0} + \beta^{T} x \leq -1$

3) 当位于超平面右边时， $f(x) = \beta_{0} + \beta^{T} x \geq +1$

假设存在一个超平面，能将 n 个样本数据正确的分类，则对于任意一个样本数据$\;(x_{i}, y_{i})$，满足如下约束条件：

$\quad y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 , i = 1, 2, ..., n $

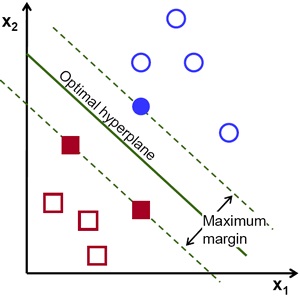
如上图所示，距离超平面最近的三个样本点，使得 2) 和 3) 中的等号成立，它们称为 “支持向量”。

2.3  几何间隔 (geometric margin)

因为支持向量使得 2) 和 3) 的等号成立，所以它们到超平面的距离：

$\quad r = \dfrac{|\beta_{0} + \beta^{T} x|} {||\beta||} = \dfrac{1}{||\beta||}$

两个不同种类的支持向量 (分别取值为 +1 和 -1)，到超平面的距离之和为：

$\quad r^{'} = \dfrac{2}{||\beta||}\;$，$r^{'}\;$称为 “几何间隔” (geometric margin)

一个点距离超平面的远近，可用来表示分类结果的正确性和确信度。

直观上看，超平面越是靠近两类样本数据的正中间 (也即两类数据点到超平面的距离越远)，则分类结果的正确性和确信度就越高。

2.4  学习算法

SVM 的学习算法 (或称最大间隔法)，就是基于所给的样本数据，去寻找到具有 “最大间隔” 的超平面，将不同种类的样本分隔开来。

也即，在满足 “约束条件” 的前提下，使得 $r^{'}$ 的值最大：

$\quad \max \limits_{\beta,\; \beta_{0}} \dfrac{2}{||\beta||} \quad subject\;to \quad y_{i}(\beta^{T} x_{i} + \beta_{0}) \geq 1 , i = 1, 2, ..., n $

再或者，最大化 $r^{'}$，等价于最小化 $||\beta||^{2}$，如下所示：

$\quad \min \limits_{\beta,\;\beta_{0}} \dfrac{1}{2} ||\beta||^{2} \quad subject \; to \quad y_{i} (\beta^{T} x_{i} + \beta_{0}) \geq 1 , i = 1, 2, ..., n $

3  OpenCV 函数

OpenCV 中 SVM 的实现是基于 libsvm 的，其基本的过程为：创建 SVM 模型 --> 设置相关参数 --> 样本数据训练 --> 预测

1) 创建模型

static Ptr<SVM> cv::ml::SVM::create ( );  // 创建一个空模型

 2) 设置参数

virtual void cv::ml::SVM::setType (int val);  // 设置 SVM 的类型，默认为 SVM::C_SVC 
virtual void cv::ml::SVM::setKernel (int kernelType); // 设置核函数类型，本文为线性核函数，设为 SVM::LINEAR

virtual void cv::ml::SVM::setTermCriteria (const cv::TermCriteria & val); // 设置迭代终止准则

// type，准则类型; maxCount，最大迭代次数；epsilo，目标精度
cv::TermCriteria::TermCriteria(int type, int maxCount, double epsilon);       

3) 训练 (train)

virtual bool cv::ml::StatModel::train (
 　　InputArray　　samples,　  // 训练样本
    int    　　　　layout,　　 // 训练样本为 “行样本” ROW_SAMPLE 或 “列样本” COL_SAMPLE
    InputArray    responses　// 对应样本数据的分类结果
)     

4) 预测 (predict)

用来预测一个新样本的响应，各个参数如下：

// samples，输入的样本书数据；results，输出矩阵，默认不输出；flags，标识，默认为 0

virtual float cv::ml::StatModel::predict(InputArray samples, OutputArray results=noArray(),int flags=) const;　　

4  代码示例

下面是 OpenCV 3.2 中的官方例程，更改了训练样本数据

#include <opencv2/core.hpp>
#include <opencv2/imgproc.hpp>
#include "opencv2/imgcodecs.hpp"
#include <opencv2/highgui.hpp>
#include <opencv2/ml.hpp>

using namespace cv;
using namespace cv::ml;

int main()
{
    // 512 x 512 零矩阵
    int width = , height = ;
    Mat image = Mat::zeros(height, width, CV_8UC3);

    // 训练样本
    float trainingData[][] = { { ,  },{ ,  },{ ,  },{ ,  },{, },{, } };
    int labels[] = {-, , , ,-,};  // 每个样本数据对应的输出，因为是二分模型，所以输出为 +1 或者 -1
    Mat trainingDataMat(, , CV_32FC1, trainingData);
    Mat labelsMat(, , CV_32SC1, labels);

    // 训练 SVM
    Ptr<SVM> svm = SVM::create();
    svm->setType(SVM::C_SVC);
    svm->setKernel(SVM::LINEAR);
    svm->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER, , 1e-));
    svm->train(trainingDataMat, ROW_SAMPLE, labelsMat);

    // 显示二分分类的结果
    Vec3b green(, , ), blue(, , );
    for (int i = ; i < image.rows; ++i)
        for (int j = ; j < image.cols; ++j)
        {
            Mat sampleMat = (Mat_<float>(, ) << j, i);
            float response = svm->predict(sampleMat);
            if (response == )
                image.at<Vec3b>(i, j) = blue;
            else if (response == -)
                image.at<Vec3b>(i, j) = green;
        }
    // 画出训练样本数据
    int thickness = -;
    int lineType = ;
    circle(image, Point(, ), , Scalar(, , ), thickness, lineType);
    circle(image, Point(, ), , Scalar(, , ), thickness, lineType);
    circle(image, Point(, ), , Scalar(, , ), thickness, lineType);
    circle(image, Point(, ), , Scalar(, , ), thickness, lineType);
    circle(image, Point(, ), , Scalar(, , ), thickness, lineType);
    circle(image, Point(, ), , Scalar(, , ), thickness, lineType);
    
    // 显示出支持向量
    thickness = 2;
    lineType = 8;
    Mat sv = svm->getUncompressedSupportVectors();
    for (int i = 0; i < sv.rows; ++i)
    {
        const float* v = sv.ptr<float>(i);
        circle(image, Point((int)v[0], (int)v[1]), 6, Scalar(128, 128, 128), thickness, lineType);
    }
    imwrite("result.png", image);        // 保存训练的结果
    imshow("SVM Simple Example", image);
    waitKey();
}

OpenCV 3.2 版本中使用了一个新的函数，来获取支持向量，即 getUncompressedSupportVectors()

而 OpenCV 3.0 中，获取支持向量的函数为 getSupportVectors()，但当内核设为 SVM::LINEAR 时，该函数并不能得到支持向量，这是 3.0 版本的缺陷。

运行结果如下图所示，超平面附近的三个灰色匡白色圆点，便是所谓的 “支持向量”。

参考资料：

<机器学习> 周志军  第6章

<统计学习方法> 李航  第7章

<The Elements of Statistical Learning_2nd>  ch 4.5 , ch 12

"支持向量机系列“  pluskid

OpenCV 3.2  Tutorials -- Machine Learning (ml module)  -- Introduction to Support Vector Machines

“LIBSVM -- A Library for Support Vector Machines”