[打基础]luogu2181对角线——计数原理

啦啦啦我ysw又回来啦！之后大概会准备打acm，暑假尽量复习复习，因为已经快两年没碰oi了，最多也就高三noip前学弟学妹出题讲题，所以从这一篇blog开始大概会有一系列“打基础”的blog，既是复习也是重新学一遍叭~高中的时候学得就不太扎实

---

题意：对于一个任何三条对角线不会交于同一点的凸$n$边形，问对角线交点个数,$n\leq 10^5$。

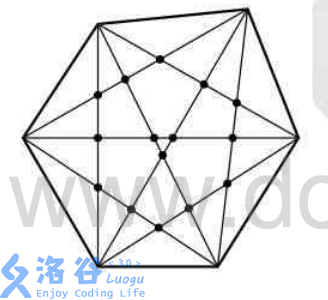
例如$n=6$的情形下答案为15

 

---

 

我来丢人啦（下面将呈现我当时整个思考过程…）

凸多边形相关的计数我们其实处理过不少，嗯比如我们如果从$n$个点中任取2个点，整个图形一共有$C_{n}^2=\frac{1}{2} n(n-1)$条边，去掉凸多边形自己一圈$n$条边，就得到对角线的条数：$\frac{1}{2}n(n-1)-n=\frac{1}{2}n(n-3)$

嗯…那我们要交点数，哦吼！那我们让对角线数*（对角线数-1）是不是就是答案了呢！等一下似乎不太对，因为这样相当于认为每条对角线都和其他对角线有交点（确实如果认为对角线是“直线”那就是这么回事了）但这题似乎是要我们对多边形内部的点计数，而一些对角线可能在多边形内部没交点（看图不难发现）…嗯那这个东西好像没什么卵用呢（

 

也许可以试试欧拉示性数定理？（平面内点数、边数、面数关系）但是面数好像更难搞…算了算了

 

嗯记住我们要求交点数…前面做法不行的原因在于处理不了那些没交点的情形，去对没交点的那些边的组合进行计数似乎更加困难…

等一下关于凸多边形我们好像还有一些处理方法

似乎我们可以随意给一个端点编号为1，按照逆时针/顺时针顺序依次编号$1,2,3……n$，这样一来我们可以先只考虑以点1为其中一个端点出发的所有对角线（图中红线）对应的交点，这个问题似乎好处理了许多，因为如果另一条对角线要和它有交点（蓝线）当且仅当蓝线的两个端点在红线的两侧！（嗯！这不就是计算几何里面判断直线是否有交点的方法嘛！？）

于是我们想，对于编号为$k$的点，1~k内从点2到点$k-1$是可以作为其中一个起点的，一共是$k-1-2+1=k-2$个点，同样的另一侧从$k+1$到$n$可以作为对角线另一点，一共是$n-(k+1)+1=n-k$个点

乘法原理得到$(k-2)(n-k)$，接着只要对所有情形进行求和就行了，对于$k$来说最小取到3（2的话就不是对角线了），最大取到$n-1$

所以对于以任意一点为端点的所有对角线的交点便是：$m=\sum_{k=3}^{n-1}(n-k)(k-2)$，对$n$个点进行同样的操作就得到$nm$，而注意到如果这样写，每个交点对应两条对角线的四个端点都作为了一次起点，也就是说每个交点都被算了四次，所以我们要的答案应该是$ans=\frac{1}{4}nm$，式子推出来啦！

---

接着就可以编程求解了…首先整个问题的时间复杂度是$O(n)$，轻轻松松通过，不过我们注意到对应答案的上界是$O(n^3)$级别的也就是$10^{15}$级别的差不多，一开始我只开了个long long交上去然后挂了两个点…后面改成unsigned long long 就过了…emm好吧

---

话说回来我们再回头看看那个和式$m=\sum_{k=3}^{n-1}(n-k)(k-2)$，好像我们并不陌生呀！

里面展开就是$nk-2n-k^2-2k$我们对k求和就稍微整理一下变成$\sum_{k=3}^{n-1}[k(n-2)-2n-k^2]$，嗯第一项是等差数列，第二项是对于$k$的常数列，第三项是平方和，我们有结论$\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)$，对于这题只要改个$n$再扣掉前两项就行

整个和式拆开再化简就得到这题的答案可以写成：

$\frac{n}{4}[\frac{1}{2}(n+2)^2-2(n^2-3n)-\frac{1}{6}n(n-1)(2n-1)+5]$

整个问题变成$O(1)$的复杂度啦！~（虽然好像没什么用，哈哈哈）