C++学习---二叉树的输入及非递归遍历

二叉树的二叉链表存储表示如下

//二叉树的二叉链表存储表示
typedef struct BiTNode {
    char data;//结点数据域
    struct BiTNode* lchild, * rchild;//左右孩子指针
}*BiTree;

根据括号表示法的字符串创建树(括号里的表示括号前结点的子结点，‘，’号左边是左子结点，右边是右子结点)

比如：a(b(d,e),c(f,g(h,i)))

表示的则是

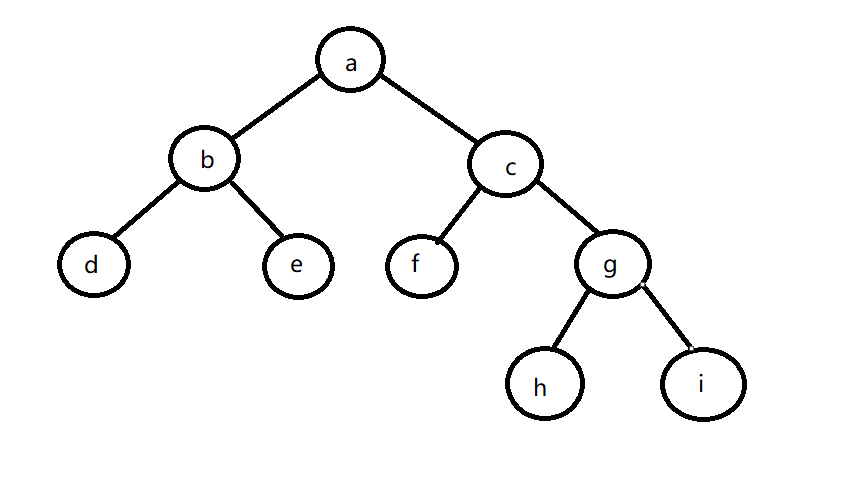
//创建树
void CreateBiTree(BiTree& T)
{
    stack<BiTNode*> s;//用于确定需要操作的结点
    BiTNode* p=NULL;
    int i = 0;
    bool child_Direct;//0表示左子结点，1表示右子结点
    //按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
    string TreeStr;
    cin >> TreeStr;
    while (TreeStr[i] != '\0') {
        switch (TreeStr[i])
        {
        case'('://左子结点
            s.push(p);
            child_Direct = false;
            break;
        case')':
            s.pop();
        case','://右子结点
            child_Direct = true;
            break;

        default:
            p = new BiTNode;
            p->data = TreeStr[i];
            p->lchild = p->rchild = NULL;
            if (T == NULL)//若根节点为空则p指向根节点
                T = p;
            else {
                if (!child_Direct)
                    s.top()->lchild = p;
                else
                    s.top()->rchild = p;
            }
            break;
        }
        i++;
    }

}

　　

非递归先序、中序、后序遍历

先序：

void PreOrderTraverse(BiTree T) {
    stack<BiTNode*> s;
    BiTNode* p = T, * q = new BiTNode();
    while (p != NULL || !s.empty()) {
        if (p)//p非空
        {
            cout << p->data;
            s.push(p);//根指针入栈
            p = p->lchild;//遍历左子树
        }
        else {
            p = s.top();
            s.pop();
            p = p->rchild;//遍历右子树
        }
    }
}

　　

中序：

//中序遍历
void InOrderTraverse(BiTree T) {
    stack<BiTNode*> s;
    BiTNode* p = T, * q = new BiTNode();
    while (p != NULL || !s.empty()) {
        if (p)//p非空
        {
            s.push(p);//根指针入栈
            p = p->lchild;//遍历左子树
        }
        else {
            p = s.top();
            s.pop();
            cout << p->data;
            p = p->rchild;//遍历右子树
        }
    }
}

　　

后序：

//后序遍历
void PostOrderTraverse(BiTree T) {
    BiTNode* p = T, * r = NULL;
    stack<BiTNode*> s;
    while (p != NULL || !s.empty()) {
        if (p != NULL) {//走到最左边
            s.push(p);
            p = p->lchild;
        }
        else {
            p = s.top();
            if (p->rchild != NULL && p->rchild != r)//右子树存在，未被访问
                p = p->rchild;
            else {
                s.pop();
                cout << p->data;
                r = p;//记录最近访问过的节点
                p = NULL;//节点访问完后，重置p指针
            }
        }//else
    }//while

}

完整代码

#include <iostream>
#include <stack>
#include <string>
using namespace std;

//二叉树的二叉链表存储表示
typedef struct BiTNode {
    char data;//结点数据域
    struct BiTNode* lchild, * rchild;//左右孩子指针
}*BiTree;

void Initial(BiTree& T) {
    T = new BiTNode;
    T = NULL;
}
//创建树
void CreateBiTree(BiTree& T)
{
    stack<BiTNode*> s;//用于确定需要操作的结点
    BiTNode* p=NULL;
    int i = 0;
    bool child_Direct;//0表示左子结点，1表示右子结点
    //按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树T
    string TreeStr;
    cin >> TreeStr;
    while (TreeStr[i] != '\0') {
        switch (TreeStr[i])
        {
        case'('://左子结点
            s.push(p);
            child_Direct = false;
            break;
        case')':
            s.pop();
        case','://右子结点
            child_Direct = true;
            break;

        default:
            p = new BiTNode;
            p->data = TreeStr[i];
            p->lchild = p->rchild = NULL;
            if (T == NULL)//若根节点为空则p指向根节点
                T = p;
            else {
                if (!child_Direct)
                    s.top()->lchild = p;
                else
                    s.top()->rchild = p;
            }
            break;
        }
        i++;
    }

}
//以括号表示法输出二叉树
void DispBTNode(BiTNode *&b)
{
    if (b != NULL)
    {
        cout<<b->data;
        if (b->lchild != NULL || b->rchild != NULL)
        {
            cout<<"(";
            DispBTNode(b->lchild);
            if (b->rchild != NULL) cout<<(",");
            DispBTNode(b->rchild);
            cout<<")";
        }
    }
}

#pragma region 递归遍历
//先序
void PreOrderTraverseR(BiTree T) {
    if (T != NULL) {
        cout << T->data;
        PreOrderTraverseR(T->lchild);
        PreOrderTraverseR(T->rchild);
    }
}
//中序
void InOrderTraverseR(BiTree T) {
    if (T != NULL) {
        InOrderTraverseR(T->lchild);
        cout << T->data;
        InOrderTraverseR(T->rchild);
    }
}
//后序
void PostOrderTraverseR(BiTree T) {
    if (T != NULL) {
        PostOrderTraverseR(T->lchild);
        PostOrderTraverseR(T->rchild);
        cout << T->data;
    }
}
#pragma endregion

#pragma region 非递归遍历
//先序遍历
void PreOrderTraverse(BiTree T) {
    stack<BiTNode*> s;
    BiTNode* p = T, * q = new BiTNode();
    while (p != NULL || !s.empty()) {
        if (p)//p非空
        {
            cout << p->data;
            s.push(p);//根指针入栈
            p = p->lchild;//遍历左子树
        }
        else {
            p = s.top();
            s.pop();
            p = p->rchild;//遍历右子树
        }
    }
}
//中序遍历
void InOrderTraverse(BiTree T) {
    stack<BiTNode*> s;
    BiTNode* p = T, * q = new BiTNode();
    while (p != NULL || !s.empty()) {
        if (p)//p非空
        {
            s.push(p);//根指针入栈
            p = p->lchild;//遍历左子树
        }
        else {
            p = s.top();
            s.pop();
            cout << p->data;
            p = p->rchild;//遍历右子树
        }
    }
}
//后序遍历
void PostOrderTraverse(BiTree T) {
    BiTNode* p = T, * r = NULL;
    stack<BiTNode*> s;
    while (p != NULL || !s.empty()) {
        if (p != NULL) {//走到最左边
            s.push(p);
            p = p->lchild;
        }
        else {
            p = s.top();
            if (p->rchild != NULL && p->rchild != r)//右子树存在，未被访问
                p = p->rchild;
            else {
                s.pop();
                cout << p->data;
                r = p;//记录最近访问过的节点
                p = NULL;//节点访问完后，重置p指针
            }
        }//else
    }//while

}
#pragma endregion
int main()
{
    BiTree b;
    Initial(b);
    //创建树
    CreateBiTree(b);
    //先序遍历
    cout << "先序遍历：";
    PreOrderTraverse(b);
    cout << endl;
    //中序遍历
    cout << "中序遍历：";
    InOrderTraverse(b);
    cout << endl;
    //后序遍历
    cout << "后序遍历：";
    PostOrderTraverse(b);
}

　　

程序示例: