人老了就比较懒，故意挑了到看起来很和蔼的题目做，然后套个spfa和dinic的模板WA了5发，人老了，可能不适合这种刺激的竞技运动了……

题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2760

Description

Given a weighted directed graph, we define the shortest path as the path who has the smallest length among all the path connecting the source vertex to the target vertex. And if two path is said to be non-overlapping, it means that the two path has no common edge. So, given a weighted directed graph, a source vertex and a target vertex, we are interested in how many non-overlapping shortest path could we find out at most.

Input

Input consists of multiple test cases. The first line of each test case, there is an integer number N (1<=N<=100), which is the number of the vertices. Then follows an N * N matrix, represents the directed graph. Each element of the matrix is either non-negative integer, denotes the length of the edge, or -1, which means there is no edge. At the last, the test case ends with two integer numbers S and T (0<=S, T<=N-1), that is, the starting and ending points. Process to the end of the file.

Output

For each test case, output one line, the number of the the non-overlapping shortest path that we can find at most, or "inf" (without quote), if the starting point meets with the ending.

Sample Input

4

0 1 1 -1

-1 0 1 1

-1 -1 0 1

-1 -1 -1 0

0 3

5

0 1 1 -1 -1

-1 0 1 1 -1

-1 -1 0 1 -1

-1 -1 -1 0 1

-1 -1 -1 -1 0

0 4

Sample Output

2

1

呃，题意和思路什么的直接看宝典吧：

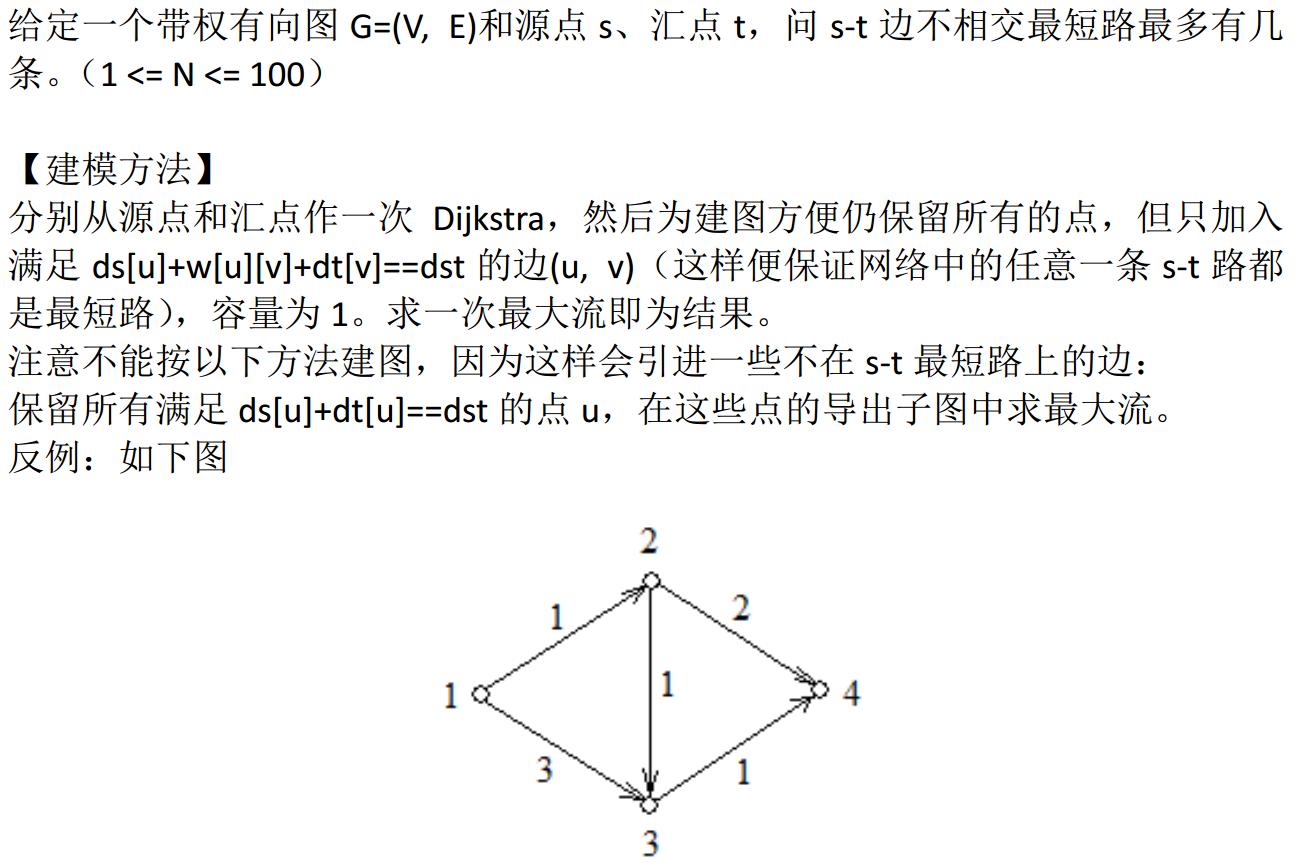
当然啦，没必要一定像他那样ds[i]+edge[i][j]+dt[j]==ds[t]这样，我们要抓住精髓，看清本质，只要保证剌进来的边属于最短路上的边就行，

所以，只要做一次spfa，然后满足d[i]+edge[i][j]==d[j]就行。

某只A题A的神志不清的博主的心灵独白                                                                   begin

然后联想到前面那题POJ1637的构图，不难发现，在integer的情况下把edge.cap设为1，可以代表一种这条边到底走不走的意义，然后全图都设为1的话，最大流大概就是……

从source到target最多有几条不相交的简单路径可走……

嗯，如果这个图上的边全是属于最短路的边的话，那么这个最大流就是本题的答案了……诶等下，再联想到dinic的BFS过程是找层次图，而层次图从某种意义上来讲就是最短路图？

所以我们可以用一个计算层次的BFS来代替SPFA？我好想发现了什么？？让我来再码一发（然而spfa本来不就是个BFS么……

然后，我立马就发现……dinic里的BFS是建立在边长默认为1的情况下的，所以我立马就放弃了我TM真是个傻子……

某只A题A的神志不清的博主的心灵独白                                                                   end

呃，先忽略我的心灵独白，看跟现在市面上比较相像的代码：

 #include<cstdio>

 #include<cstring>

 #include<queue>

 #define MAXN 103

 #define INF 0x3f3f3f3f

 using namespace std;

 int n,s,t;

 int d[MAXN],map[MAXN][MAXN];

 bool vis[MAXN];

 void spfa(int st)

 {

     for(int i=;i<n;i++){

         i==st ? d[i]= : d[i]=INF;

         vis[i]=;

     }

     queue<int> q;

     q.push(st);

     vis[st]=;

     while(!q.empty())

     {

         int u=q.front();q.pop();vis[u]=;

         for(int v=;v<n;v++)

         {

             if(u==v || map[u][v]==-) continue;

             int tmp=d[v];

             if(d[v]>d[u]+map[u][v]) d[v]=d[u]+map[u][v];

             if(d[v]<tmp && !vis[v]) q.push(v),vis[v]=;

         }

     }

 }

 struct Edge{

     int u,v,c,f;

 };

 struct Dinic

 {

     vector<Edge> E;

     vector<int> G[MAXN];

     bool vis[MAXN]; //BFS使用

     int lev[MAXN];//记录层次

     int cur[MAXN]; //当前弧下标

     void init(int n)

     {

         E.clear();

         for(int i=;i<n;i++) G[i].clear();

     }

     void addedge(int from,int to,int cap)

     {

         E.push_back((Edge){from,to,cap,});

         E.push_back((Edge){to,from,,});

         int m=E.size();

         G[from].push_back(m-);

         G[to].push_back(m-);

     }

     bool bfs()

     {

         memset(vis,,sizeof(vis));

         queue<int> q;

         q.push(s);

         lev[s]=;

         vis[s]=;

         while(!q.empty())

         {

             int now=q.front(); q.pop();

             for(int i=;i<G[now].size();i++)

             {

                 Edge edge=E[G[now][i]];

                 int nex=edge.v;

                 if(!vis[nex] && edge.c>edge.f)//属于残存网络的边

                 {

                     lev[nex]=lev[now]+;

                     q.push(nex);

                     vis[nex]=;

                 }

             }

         }

         return vis[t];

     }

     int dfs(int now,int aug)//now表示当前结点，aug表示目前为止的最小残量

     {

         if(now==t || aug==) return aug;//aug等于0时及时退出，此时相当于断路了

         int flow=,f;

         for(int& i=cur[now];i<G[now].size();i++)//从上次考虑的弧开始，注意要使用引用，同时修改cur[now]

         {

             Edge& edge=E[G[now][i]];

             int nex=edge.v;

             if(lev[now]+ == lev[nex] && (f=dfs(nex,min(aug,edge.c-edge.f)))>)

             {

                 edge.f+=f;

                 E[G[now][i]^].f-=f;

                 flow+=f;

                 aug-=f;

                 if(!aug) break;//aug等于0及时退出，当aug!=0,说明当前节点还存在另一个增广路分支

             }

         }

         return flow;

     }

     int maxflow()//主过程

     {

         int flow=;

         while(bfs())//不停地用bfs构造分层网络，然后用dfs沿着阻塞流增广

         {

             memset(cur,,sizeof(cur));

             flow+=dfs(s,INF);

         }

         return flow;

     }

 }dinic;

 int main()

 {

     while(scanf("%d",&n)!=EOF)

     {

         for(int i=;i<n;i++) for(int j=;j<n;j++) scanf("%d",&map[i][j]);

         scanf("%d%d",&s,&t);

         if(s==t)

         {

             printf("inf\n");

             continue;

         }

         spfa(s);

         dinic.init(n);

         for(int i=;i<n;i++)

             for(int j=;j<n;j++)

                 if(i!=j && map[i][j]!=- && d[i]!=INF && d[j]!=INF && d[i]+map[i][j]==d[j]) dinic.addedge(i,j,);

         printf("%d\n",dinic.maxflow());

     }

 }

（dinic模板的中文注释懒得去掉了，反正看起来不多，到时候忘记了过程还可以看看注释回忆回忆……）

ZOJ 2760 - How Many Shortest Path - [spfa最短路][最大流建图]的更多相关文章

  1. ZOJ 2760 How Many Shortest Path（Dijistra + ISAP 最大流）

    题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1760 题意:给定一个带权有向图 G=(V, E)和源点 s.汇点 t ...

  2. zoj 2760 How Many Shortest Path 最大流

    题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1760 Given a weighted directed graph ...

  3. ZOJ 2760 How Many Shortest Path（最短路径+最大流）

    Description Given a weighted directed graph, we define the shortest path as the path who has the sma ...

  4. zoj 2760 How Many Shortest Path【最大流】

    不重叠最短路计数. 先弗洛伊德求一遍两两距离(其实spfa或者迪杰斯特拉会更快但是没必要懒得写),然后设dis为st最短距离,把满足a[s][u]+b[u][v]+a[v][t]==dis的边(u,v ...

  5. ZOJ 2760 How Many Shortest Path (不相交的最短路径个数)

    [题意]给定一个N(N<=100)个节点的有向图,求不相交的最短路径个数(两条路径没有公共边). [思路]先用Floyd求出最短路,把最短路上的边加到网络流中,这样就保证了从s->t的一个 ...

  6. ZOJ 2760 How Many Shortest Path

    题目大意:给定一个带权有向图G=(V, E)和源点s.汇点t,问s-t边不相交最短路最多有几条.(1 <= N <= 100) 题解:从源点汇点各跑一次Dij,然后对于每一条边(u,v)如 ...

  7. HDU - 3631 Shortest Path(Floyd最短路)

    Shortest Path Time Limit: 1000MS Memory Limit: 32768KB 64bit IO Format: %I64d & %I64u SubmitStat ...

  8. CF843D Dynamic Shortest Path spfa+剪枝

    考试的T3,拿暴力+剪枝卡过去了. 没想到 CF 上也能过 ~ code: #include <bits/stdc++.h> #define N 100004 #define LL lon ...

  9. ZOJ 3781 - Paint the Grid Reloaded - [DFS连通块缩点建图+BFS求深度][第11届浙江省赛F题]

    题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3781 Time Limit: 2 Seconds      Me ...

随机推荐

  1. Java用三元运算符判断奇数和偶数

    创建一个类,在该类的主方法中创建标准输入流的扫描器对象,提示用户输入一个整数,并通过扫描器的方法来接受这个整数,然后通过三元运算符判断该数字与2的余数,如果余数为0,说明其是偶数,否则是奇数. imp ...

  2. iOS App Extensions

    一.扩展概述 扩展(Extension)是iOS 8中引入的一个非常重要的新特性.扩展让app之间的数据交互成为可能.用户可以在app中使用其他应用提供的功能,而无需离开当前的应用. 在iOS 8系统 ...

  3. 【内网渗透笔记】Windows2008 R2搭建域控制器

    0x00 前言 将网络中的多台计算机逻辑上组织到一起,进行集中管理,这种区别于工作组的逻辑环境叫做域(domain).域是日常计算机管理的一种很有效手段,因此,域控制器自然而然就在成域环境中最重要的角 ...

  4. 使用 Selenium

    Selenium 简介 Selenium 基本用法 Selenium 查找节点 Selenium 节点交互 Selenium 动作链 Selenium 执行 JavaScript Selenium 获 ...

  5. angular-file-upload+struts的使用

    参考帖子 http://www.cnblogs.com/wangzun/p/6099884.html http://www.cnblogs.com/highriver/archive/2011/06/ ...

  6. 【Java知识点专项练习】之 接口和抽象类的区别

    接口和抽象类的区别 接口(interface)可以说成是抽象类的一种特例,接口中的所有方法都必须是抽象的.接口中的方法定义默认为public abstract类型,接口中的成员变量类型默认为publi ...

  7. JS动态设置确认弹窗

    多次使用确认弹窗 <!--START 确认收货--> <div class="popout-boxbg out" id="delivery_goods& ...

  8. 【调试错误】找不到 System.Web.Mvc 引用

    今天调试新项目,从svn上clone下来,发现运行不了. System.Web.Mvc 显示黄色叹号 解决方案如下: 安装一个 MVC 的插件.AspNetMVC2_VS2008.exe 下载地址:h ...

  9. 【vue基础学习】vue.js开发环境搭建

    1.安装node.js(http://www.runoob.com/nodejs/nodejs-install-setup.html) 2.基于node.js,利用淘宝npm镜像安装相关依赖 在cmd ...

  10. 【Linux】使用 telnet 提示 Escape character is '^]'的意义

    在linux/unix下使用telnet hostname port连接上主机后会提示Escape character is '^]' 这个提示的意思是按Ctrl + ] 会呼出telnet的命令行, ...