LG3898 [湖南集训]大新闻
题意
题目描述
**记者弄了个大新闻,这个新闻是一个在 [0,n) 内等概率随机选择的整数,记其为 x。为了尽可能消除这个大新闻对公众造成的不良印象,我们需要在 [0,n)内找到某一个整数 y,使得 x ⊕ y 达到最大值。这里 ⊕ 代表异或。
问题在于,**记者有可能对大新闻进行了加密。情报显示,大新闻没有被加密的概率为 p。我们决定采取这样的策略:如果大新闻没有被加密,那么我们选出使得 x ⊕ y 最大的 y;否则,我们在 [0,n) 内等概率随机选择一个整数作为 y。
请求出 x ⊕ y 的期望值。
输入输出格式
输入格式:
输入文件仅包含一行,其中有一个正整数 n 和一个实数 p,含义如问题描述中所述。 p 至多精确到小数点后六位。
输出格式:
输出一行,代表 x ⊕ y 的期望值。只有当你的输出与标准输出的相对误差不超过 10−510^{-5}10−5 时,你的输出才会被判为正确。建议保留至少六位小数。
输入输出样例
说明
考虑样例一。如果大新闻没有被加密,那么可能的 x 与对应的 y 的取值如下:
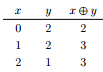
此时的期望值为 8/3。
如果大新闻被加密了,那么可能的 x 和 y 的取值如下:
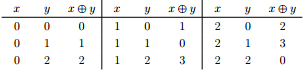
此时的期望值为 12/9 = 4/3。
所以总的期望值为 2。
所有测试点的数据规模如下:

对于全部测试数据,1≤n≤10181 \le n \le 10^{18}1≤n≤1018。
分析
参照[]
首先我们打一个i^j的表
我们发现,第一,这是一个关于对角线对称的(废话)
第二,对于任意一个从左上角开始,边长为2的幂的正方形(比如图中用白框框起来的),其下边和右边的边长为2的幂的正方形就是把这个正方形的每个元素加上这个2的幂
第三,对于任意一个从左上角开始,边长为2的幂的正方形,其右下的边长为2的幂的正方形和这个正方形是一样的
第四,对于从顶部开始,向下长度为2的幂的一列,0到2的幂-1的所有数都恰好出现一次
发现了这些规律之后我们看题,当p=1的时候,相当于求从第一列开始n列每列的最大值的和/n,p=0的时候,相当于求从左上角开始nn的正方形内所有元素的和/(nn)
当0<p<1时,只要把上边两个值加权加起来即可
先说如何求n*n的正方形的和
找到小于等于n的最大的2的幂的正方形,左上角的正方形可由规律4直接求出,右上的长方形可由规律2和规律4直接求出,由规律1左下的长方形和右上的长方形和是一样的,然后由规律3,我们可以递归求右下的正方形,这样复杂度是log的
在说如何求n列里每列最大值的和
找到小于n的最大的2的幂的正方形,由规律2和3,可知最大值一定在左下和右上,由规律4右上部分的可以直接求,然后我们递归左下的长方形
这样递归就有了3个变量x,y,u,x代表有多少行,y代表有多少列,u代表又规律2现在这个递归部分被加了多少值
在进行一次递归之后,y一定是2的幂
找到小于y的最大的2的幂xx,这里分两种情况讨论,若x>xx,即有左下部分,则算出右上然后递归左下,若x<=xx,即没有左下部分,由规律2我们递归左半边,然后右半边可以根据左半边的直接算出来
然后就好了
代码
其实要理解思路把代码和图结合起来看蛮清晰的。
但是他卡精度我是一点办法都没有,此题留坑吧。
#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;
rg char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') w=-1;
ch=getchar();
}
while(isdigit(ch))
data=data*10+ch-'0',ch=getchar();
return data*w;
}
template<class T>il T read(rg T&x){
return x=read<T>();
}
typedef __int128 ll;
typedef long double ld;
class fraction{
private:
ll numerator;//分子
ll denominator;//分母
ll gcd(ll x,ll y)const;//最大公约数
ll lcm(ll x,ll y)const;//最小公倍数
void fixup();//维护分母始终为正数
public:
//构造函数
fraction();//缺省构造函数
fraction(ll numerator); //分母默认值为1
fraction(ll numerator,ll denominator);
//运算符重载
friend const fraction operator +(const fraction &x,const fraction &y);
friend const fraction operator -(const fraction &x,const fraction &y);
friend const fraction operator *(const fraction &x,const fraction &y);
friend const fraction operator /(const fraction &x,const fraction &y);
const fraction operator -();
const fraction simplify()const; //化简
const fraction reciprocal()const;//倒数
friend bool operator >(const fraction &x,const fraction &y);
friend bool operator >=(const fraction &x,const fraction &y);
friend bool operator <(const fraction &x,const fraction &y);
friend bool operator <=(const fraction &x,const fraction &y);
friend bool operator !=(const fraction &x,const fraction &y);
friend bool operator ==(const fraction &x,const fraction &y);
fraction& operator =(const fraction &x);
//输出
ld print()const;
};
//用初始化列表写构造函数
fraction::fraction(ll x,ll y):numerator(x),denominator(y){
assert(y!=0);//确保分母不为0,否则在运行过程中报错
}
fraction::fraction(ll x):numerator(x),denominator(1){ }
fraction::fraction(){ }
//最小公倍数
ll fraction::lcm(ll x,ll y)const
{
//欧几里得算法
while(y){
ll t=y;
y=x%y;
x=t;
}
return x;
}
//最大公约数
ll fraction::gcd(ll x,ll y)const
{
ll n=lcm(x,y);
return x*y/n;
}
//维护分母为正
void fraction::fixup()
{
//如果分母为负,将分子分母同时取负
if(denominator<0){
denominator=-denominator;
numerator=-numerator;
}
assert(denominator!=0);
}
//化简
const fraction fraction::simplify()const
{
fraction ans;
ll n=lcm(numerator,denominator);//得到最小公倍数
ans.denominator=denominator/n;//分子分母同时除以最小公倍数
ans.numerator=numerator/n;
return ans;
}
const fraction operator +(const fraction &x,const fraction &y)
{
ll n=x.gcd(x.denominator,y.denominator);//得到最大公约数
fraction ans;
//将分母化为相同的再对分子进行加法运算
ans.numerator=n/x.denominator*x.numerator+n/y.denominator*y.numerator;
ans.denominator=n;
return ans.simplify();
}
const fraction operator -(const fraction &x,const fraction &y)
{
ll n=x.gcd(x.denominator,y.denominator);//得到最大公约数
fraction ans;
//将分母化为相同的再对分子进行减法运算
ans.numerator=n/x.denominator*x.numerator-n/y.denominator*y.numerator;
ans.denominator=n;
return ans.simplify();
}
const fraction operator *(const fraction &x,const fraction &y)
{
fraction ans;
fraction tmp_x=x.simplify();
fraction tmp_y=y.simplify();
//分子分母对应相乘
ans.numerator=tmp_x.numerator*tmp_y.numerator;
ans.denominator=tmp_x.denominator*tmp_y.denominator;
return ans.simplify();
}
const fraction operator /(const fraction &x,const fraction &y)
{
fraction ans;
fraction tmp_x=x.simplify();
fraction tmp_y=y.simplify();
assert(tmp_y.denominator!=0);//分子为0不能作为除数
//分子乘分母,分母乘分子
ans.numerator=tmp_x.numerator*tmp_y.denominator;
ans.denominator=tmp_x.denominator*tmp_y.numerator;
ans=ans.simplify();
ans.fixup();
return ans;
}
const fraction fraction::operator -()
{
//分子变为相反数
fraction x;
x.numerator=-numerator;
x.denominator=denominator;
return x;
}
fraction& fraction::operator =(const fraction &x)
{
if(this!=&x){
numerator=x.numerator;
denominator=x.denominator;
}
return *this;
}
bool operator >(const fraction &x,const fraction &y)
{
if((x-y).numerator>0)return true;
else return false;
}
bool operator >=(const fraction &x,const fraction &y)
{
if((x-y).numerator>=0)return true;
else return false;
}
bool operator <(const fraction &x,const fraction &y)
{
if((x-y).numerator<0)return true;
else return false;
}
bool operator <=(const fraction &x,const fraction &y)
{
if((x-y).numerator<=0)return true;
else return false;
}
bool operator !=(const fraction &x,const fraction &y)
{
if((x-y).numerator!=0)return true;
else return false;
}
bool operator ==(const fraction &x,const fraction &y)
{
if((x-y).numerator==0)return true;
else return false;
}
const fraction fraction::reciprocal()const
{
return 1/(*this);
}
ld fraction::print()const
{
return (ld)numerator/denominator;
}
ll n;
ld p;
ll low(ll x){
ll t=1;
for(;t<=x;t<<=1);
return t>>1;
}
fraction sum(ll x,ll y){
return fraction(x+y)*(y-x+1)/2;
}
fraction cal2(ll x){
if(x<=1) return 0;
ll xx=low(x);
return sum(0,xx-1)*xx+sum(xx,xx+xx-1)*(x-xx)*2+cal2(x-xx);
}
fraction cal1(ll x,ll y,ll u){
if(!x||!y) return 0;
if(y==1) return u;
ll xx=low(y-1);
if(x>xx) return (u+xx*2-1)*(y-xx)+cal1(x-xx,xx,u+xx);
return cal1(x,xx,u)*2+xx*xx;
}
int main(){
// freopen(".in","r",stdin),freopen(".out","w",stdout);
read(n);
scanf("%Lf",&p);
printf("%Lf\n",p*cal1(n,n,0).print()/n+(1-p)*cal2(n).print()/n/n);
return 0;
}正解
很久以前,某出题人给我们考了一套题,里面就有。
这并不是古典概型……
LG3898 [湖南集训]大新闻的更多相关文章
- 大新闻!HoloLens即将入华商用
昨天微软搞了大新闻,Terry和Alexi到了深圳,在WinHEC大会上宣布了2017上半年HoloLens正式入华商用. 关于HoloLens的技术原理和细节官方文档和报道已经披露很多了,他是一款真 ...
- 主席树 || 可持久化线段树 || BZOJ 3653: 谈笑风生 || Luogu P3899 [湖南集训]谈笑风生
题面:P3899 [湖南集训]谈笑风生 题解: 我很喜欢这道题. 因为A是给定的,所以实质是求二元组的个数.我们以A(即给定的P)作为基点寻找答案,那么情况分两类.一种是B为A的父亲,另一种是A为B的 ...
- [BZOJ 3652]大新闻
[BZOJ 3652] 大新闻 题意 随机从 \([0,n)\) 中选取一个整数 \(x\), 并从 \([0,n)\) 中再选取一个整数 \(y\). 有 \(p\) 的概率选取一个能令 \(x\o ...
- P3900 [湖南集训]图样图森破
P3900 [湖南集训]图样图森破 链接 分析: 感觉像个暴力. 可以枚举回文串的回文中心,即枚举一个串,枚举一个串的位置作为回文中心,然后求出这个串内的回文串的长度. 此时如果回文串两端都没有到这个 ...
- 【python】10分钟教你用python一行代码搞点大新闻
准备 相信各位对python的语言简洁已经深有领会了.那么,今天就带大家一探究竟.看看一行python代码究竟能干些什么大新闻.赶紧抄起手中的家伙,跟我来试试吧. 首先你得先在命令行进入python. ...
- [CSP-S模拟测试]:大新闻(主席树)
题目传送门(内部题20) 输入格式 第一行为两个数$n,m$,意义如题所述.接下来一行$n$个数,代表一开始$n$条大新闻的$naive$值.接下来$m$行,每行一个操作,输入格式如下:读入$1$,代 ...
- 几年前的今天,Google发了这几篇“大”新闻
免责声明: 因阅读本文所导致的任何时间或经济上的损失,皆由您自行承担,本小编概不负责. 估计今天我的朋友圈会被"震惊!"刷屏,来看看 Google 做过哪些令人"震惊&q ...
- 湖南集训day2
难度:☆☆ /*显然可以前缀和*/ #include<iostream> #include<cstdio> #include<cstring> #define N ...
- CDQZ 集训大总结
好爆炸的一次集训…… 成绩: 什么鬼, 烂到一定地步了. 在这里每天考试80%都是暴力,正解思维难度的确比之前大了很多,考的范围也扩大了,比起之前的单独考一个知识点,转变为了多知识点多思维的综合,见了 ...
随机推荐
- LeetCode--217--存在重复元素
问题描述: 给定一个整数数组,判断是否存在重复元素. 如果任何值在数组中出现至少两次,函数返回 true.如果数组中每个元素都不相同,则返回 false. 示例 1: 输入: [1,2,3,1] 输出 ...
- codeforces 555b//Case of Fugitive// Codeforces Round #310(Div. 1)
题意:有n-1个缝隙,在上面搭桥,每个缝隙有个ll,rr值,ll<=长度<=rr的才能搭上去.求一种搭桥组合. 经典问题,应列入acm必背300题中.属于那种不可能自己想得出来的题.将二元 ...
- Mashmokh and ACM CodeForces - 414D (贪心)
大意: 给定n结点树, 有k桶水, p块钱, 初始可以任选不超过k个点(不能选根结点), 在每个点放一桶水, 然后开始游戏. 游戏每一轮开始时, 可以任选若干个节点关闭, 花费为关闭结点储存水的数量和 ...
- FasfDFS intall nginx with image filter
centOS7 x64 1. install gd-devel 2. ./configure --prefix=/usr/local/nginx --with-http_image_filter_mo ...
- UI线程和工作者线程
本文转载于:http://blog.csdn.net/libaineu2004/article/details/40398405 1.线程分为UI线程和工作者线程,UI线程有窗口,窗口自建了消息队列, ...
- Oracle11g温习-第四章:手工建库
1.create database plan 1.库类型: OLTP : 在线事务处理系统 OLAP : 在线应用处理系统 DSS : 数据决策系统 2.数据库名字及字符集 3. ...
- 获取当前目录getcwd,设置工作目录chdir,获取目录信息
#include <unistd.h> #include <stdio.h> #include <limits.h> int main(int argc, char ...
- BZOJ1907 树的路径覆盖
ydc题解上写着贪心,后来又说是树形dp...可惜看不懂(顺便骗三连) 其实就是每个叶子开始拉一条链,从下面一路走上来,遇到能把两条链合起来的就合起来就好了. /******************* ...
- linux physical and virtual addressing modes
example 1: 特理地址和虚拟地址一致 Physical addressing mode requires no page tables and the CPU does not attempt ...
- (zz)设置单元格的宽度和高度
(zz)设置单元格的宽度和高度 博客分类: POI生成Excel 在Excel中,单元格的宽度其实就是列的宽度,因为Excel假设这一列的单元格的宽度肯定一致.所以要设置单元格的宽度,我们就得从列 ...

